How to Sort a LinkedList in Java?
Last Updated :
13 Feb, 2023
A Linked List is a linear data structure, in which the elements are not stored at contiguous memory locations.
Sorting the nodes of a Singly Linked list in ascending order:

Original List
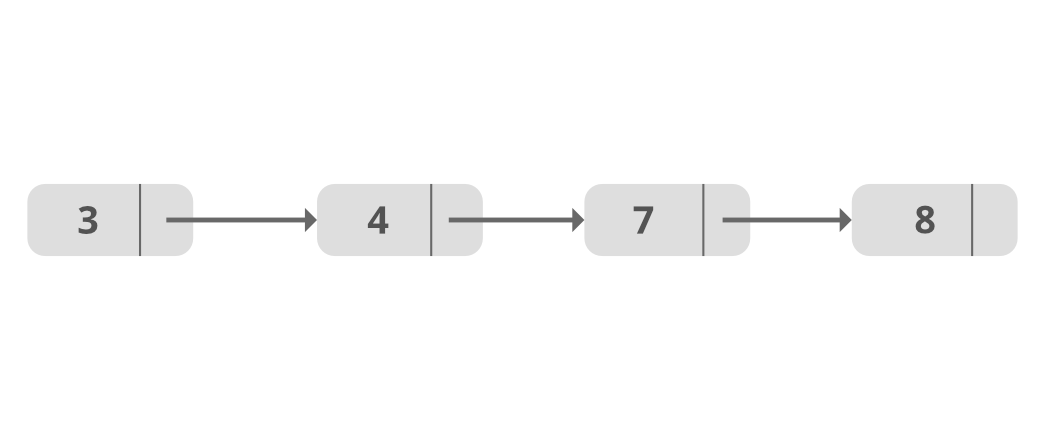
Sorted List
We can sort the LinkedList by many sorting techniques:
- Bubble sort
- Insertion sort
- Quick sort
- Merge sort
Method 1: Sort Linked List using Bubble Sort
- To accomplish this task, we maintain two pointers: current and index.
- Initially, current point to head node and index will point to node next to current.
- Traverse through the list till current points to null, by comparing current’s data with index’s data.
- And for each current’s value, index is the next to current node which traverse from current’s next node till null.
- And then the value of current node is compared with every value from its next node till last and if the value is smaller than the current value, then the values are swapped and in this way the least value comes as current index.
Java
public class SortList {
class Node {
int data;
Node next;
public Node(int data)
{
this.data = data;
this.next = null;
}
}
public Node head = null;
public Node tail = null;
public void addNode(int data)
{
Node newNode = new Node(data);
if (head == null) {
head = newNode;
tail = newNode;
}
else {
tail.next = newNode;
tail = newNode;
}
}
public void sortList()
{
Node current = head, index = null;
int temp;
if (head == null) {
return;
}
else {
while (current != null) {
index = current.next;
while (index != null) {
if (current.data > index.data) {
temp = current.data;
current.data = index.data;
index.data = temp;
}
index = index.next;
}
current = current.next;
}
}
}
public void display()
{
Node current = head;
if (head == null) {
System.out.println("List is empty");
return;
}
while (current != null) {
System.out.print(current.data + " ");
current = current.next;
}
System.out.println();
}
public static void main(String[] args)
{
SortList sList = new SortList();
sList.addNode(8);
sList.addNode(3);
sList.addNode(7);
sList.addNode(4);
System.out.println("Original list: ");
sList.display();
sList.sortList();
System.out.println("Sorted list: ");
sList.display();
}
}
|
Output
Original list:
8 3 7 4
Sorted list:
3 4 7 8
Time complexity: O(n ^ 2)
Auxiliary Space: O(1)
Method 2: Sort Linked List using Insertion Sort
- In the Insertion sort technique, we assume that all the elements before the current element in the list is already sorted, and we begin with the current element.
- The current element is compared with all the elements before it and swapped if not in order. This process is repeated for all the subsequent elements.
- In general, the Insertion sort technique compares each element with all of its previous elements and sorts the element to place it in its proper position.
As already mentioned, the Insertion sort technique is more feasible for a smaller set of data, and thus arrays with a few elements can be sorted using efficiently Insertion sort.
Insertion sort is especially useful in sorting linked list data structures. As you know, Linked lists have pointers pointing to its next element (singly linked list) and previous element (double linked list). This makes it easier to keep track of the previous and next elements.
Java
public class LinkedlistIS {
node head;
node sorted;
class node {
int val;
node next;
public node(int val) { this.val = val; }
}
void push(int val)
{
node newnode = new node(val);
newnode.next = head;
head = newnode;
}
void insertionSort(node headref)
{
sorted = null;
node current = headref;
while (current != null) {
node next = current.next;
sortedInsert(current);
current = next;
}
head = sorted;
}
void sortedInsert(node newnode)
{
if (sorted == null || sorted.val >= newnode.val) {
newnode.next = sorted;
sorted = newnode;
}
else {
node current = sorted;
while (current.next != null
&& current.next.val < newnode.val) {
current = current.next;
}
newnode.next = current.next;
current.next = newnode;
}
}
void printlist(node head)
{
while (head != null) {
System.out.print(head.val + " ");
head = head.next;
}
}
public static void main(String[] args)
{
LinkedlistIS list = new LinkedlistIS();
list.push(4);
list.push(7);
list.push(3);
list.push(8);
System.out.println("Linked List before Sorting..");
list.printlist(list.head);
list.insertionSort(list.head);
System.out.println("\nLinkedList After sorting");
list.printlist(list.head);
}
}
|
Output
Linked List before Sorting..
8 3 7 4
LinkedList After sorting
3 4 7 8
Time complexity: O(n ^ 2)
Auxiliary Space: O(1)
Method 3: Sort Linked List using Quick Sort
Quick sort follows divide and conquer approach. It picks an element as pivot and partitions the given array around the picked pivot.
The key process in quickSort is partition(). Target of partitions is, given an array and an element x of array as pivot, put x at its correct position in sorted array and put all smaller elements (smaller than x) before x, and put all greater elements (greater than x) after x. All this should be done in linear time.
Quick sort is preferred over merge sort as Quick sort is an in-place algorithm (meaning, no additional memory space required).
Java
public class QuickSortLinkedList {
static class Node {
int data;
Node next;
Node(int d)
{
this.data = d;
this.next = null;
}
}
Node head;
void addNode(int data)
{
if (head == null) {
head = new Node(data);
return;
}
Node curr = head;
while (curr.next != null)
curr = curr.next;
Node newNode = new Node(data);
curr.next = newNode;
}
void printList(Node n)
{
while (n != null) {
System.out.print(n.data);
System.out.print(" ");
n = n.next;
}
}
Node paritionLast(Node start, Node end)
{
if (start == end || start == null || end == null)
return start;
Node pivot_prev = start;
Node curr = start;
int pivot = end.data;
while (start != end) {
if (start.data < pivot) {
pivot_prev = curr;
int temp = curr.data;
curr.data = start.data;
start.data = temp;
curr = curr.next;
}
start = start.next;
}
int temp = curr.data;
curr.data = pivot;
end.data = temp;
return pivot_prev;
}
void sort(Node start, Node end)
{
if (start == end)
return;
Node pivot_prev = paritionLast(start, end);
sort(start, pivot_prev);
if (pivot_prev != null && pivot_prev == start)
sort(pivot_prev.next, end);
else if (pivot_prev != null
&& pivot_prev.next != null)
sort(pivot_prev.next.next, end);
}
public static void main(String[] args)
{
QuickSortLinkedList list
= new QuickSortLinkedList();
list.addNode(8);
list.addNode(3);
list.addNode(7);
list.addNode(4);
Node n = list.head;
while (n.next != null)
n = n.next;
System.out.println("Original List: ");
list.printList(list.head);
list.sort(list.head, n);
System.out.println("\nSorted List: ");
list.printList(list.head);
}
}
|
Output
Original List:
8 3 7 4
Sorted List:
3 4 7 8
Time complexity: O(n ^ 2)
Auxiliary Space: O(1)
Method 3: Sort Linked List using Merge Sort
Merge sort is often preferred for sorting a linked list. The slow random-access performance of a linked list makes some other algorithms (such as quicksort) perform poorly, and others (such as heapsort) completely impossible.
Merge Sort is a Divide and Conquer algorithm. It divides the input array into two halves, calls itself for the two halves, and then merges the two sorted halves. The merge() function is used for merging two halves. The merge(arr, l, m, r) is a key process that assumes that arr[l..m] and arr[m+1..r] are sorted and merges the two sorted sub-arrays into one.
- Let head be the first node of the linked list to be sorted and headRef be the pointer to head.
- Note that we need a reference to head in MergeSort() as the below implementation changes next links to sort the linked lists (not data at the nodes), so head node has to be changed if the data at original head is not the smallest value in linked list.
Java
public class linkedList {
node head = null;
static class node {
int val;
node next;
public node(int val) { this.val = val; }
}
node sortedMerge(node a, node b)
{
node result = null;
if (a == null)
return b;
if (b == null)
return a;
if (a.val < b.val) {
result = a;
result.next = sortedMerge(a.next, b);
}
else {
result = b;
result.next = sortedMerge(a, b.next);
}
return result;
}
node mergeSort(node h)
{
if (h == null || h.next == null) {
return h;
}
node middle = getMiddle(h);
node nextofmiddle = middle.next;
middle.next = null;
node left = mergeSort(h);
node right = mergeSort(nextofmiddle);
node sortedlist = sortedMerge(left, right);
return sortedlist;
}
public static node getMiddle(node head)
{
if (head == null)
return head;
node slow = head, fast = head;
while (fast.next != null
&& fast.next.next != null) {
slow = slow.next;
fast = fast.next.next;
}
return slow;
}
void push(int new_data)
{
node new_node = new node(new_data);
new_node.next = head;
head = new_node;
}
void printList(node headref)
{
while (headref != null) {
System.out.print(headref.val + " ");
headref = headref.next;
}
}
public static void main(String[] args)
{
linkedList li = new linkedList();
li.push(4);
li.push(7);
li.push(3);
li.push(8);
System.out.print("\nOriginal List: \n");
li.printList(li.head);
li.head = li.mergeSort(li.head);
System.out.print("\nSorted List: \n");
li.printList(li.head);
}
}
|
Output
Original List:
8 3 7 4
Sorted List:
3 4 7 8
Time complexity: O(n log n)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...