How to Iterate through each element in N-Dimensional matrix in MATLAB?
Last Updated :
20 Oct, 2021
In MATLAB, a matrix is considered a two-dimensional array of numbers. Other programming languages work with numbers but in MATLAB, every number is a matrix or array. To create a matrix in MATLAB, numbers are entered in each row by adding a comma or space and the ending of each row is marked by a semicolon.
Suppose, the following code created a matrix of 2-by-2:
Example:
Output:
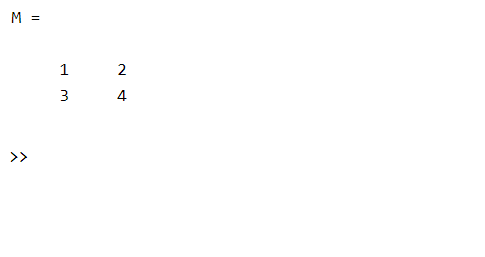
Method 1
In this method, we iterate a matrix when you need to keep track of the index at which you are currently at present.
Example:
Matlab
M = [2 3 4 5;
6 7 8 9 ;
0 1 6 8];
[rows,column]=size(M);
for i=1:rows
for j=1:column
x=M(i,j);
fprintf( ' %d ',x);
end
fprintf('\n');
end
|
Output:

output matrix
Method 2
The above method to iterate a matrix is used when you need to keep track of the index at which you are currently at present. There is another way to iterate a matrix using a semicolon. In the matrix, as discussed above, each element can be accessed by specifying its position in the matrix. If you want to iterate through some specific elements use range based indexing as illustrates below:
Example 1:
Matlab
M=[2 3 4 5; 6 7 8 9 ; 0 1 6 8];
M(2:3,1:2)
|
Output:

OUTPUT
Similarly, the whole matrix can be iterated by using range based indexing as:
Example 2:
Matlab
M=[2 3 4 5; 6 7 8 9 ; 0 1 6 8];
M(1:3,1:4)
|
Output:
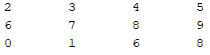
OUTPUT
Extending the above idea, the whole matrix can be iterated without explicitly defining range vectors as shown below:
Example 3:
Matlab
M=[2 3 4 5; 6 7 8 9 ; 0 1 6 8];
M(:,:)
|
Output:
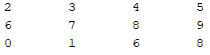
OUTPUT
Method 3
In MATLAB there is a function numel that can give the number of elements in a matrix. Using it iterate through the matrix and display each element of the matrix as shown below:
Example:
Matlab
M=[2 3 4 5; 6 7 8 9 ; 0 1 6 8];
output=[];
n=numel(M);
for i=1:n
output(i)=M(i);
end
output
|
Output:
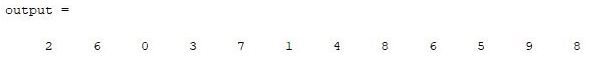
OUTPUT
Here the output is different from above because elements of a matrix are accessed column-wise. As the loop goes from 1 to a number of elements in the matrix, every element is accessed according to its index. The table shows the linear indexing of each element in the MATLAB matrix.
| 1 |
4 |
7 |
10 |
| 2 |
5 |
8 |
11 |
| 3 |
6 |
9 |
12 |
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...