How to find the perimeter and area of a triangle?
Last Updated :
13 Dec, 2021
Geometry is a branch of mathematics as old as arithmetic itself. It deals with the properties of figures, their measurements, the distance between two shapes or points, and their relative positions. In other words, geometry is a branch of mathematics that deals with surfaces, points, shapes, planes, coordinates, etc. Every kind of shape observed in nature falls under the scope of geometry. It helps measure various proportions of all such shapes and calculate their areas, volumes, and other parameters associated with them. Not only does it help one steer clear through mathematical theory, but also proves useful in daily lives as well.
Triangle
A triangle is defined as a flat shape that is obtained by joining three points, two of which are non-collinear. In case all three points turn out to be collinear, the resultant figure would not be called a triangle. As the name suggests, a triangle has three angles, the sum of which always measures 180 degrees. Since it is an enclosed figure formed by joining three co-planar points, a triangle is a two- dimensional shape, implying it is a flat shape devoid of any thickness.
The following figure depicts a triangle ABC with three vertices AB, BC, and CA.

Types of Triangles
- Scalene Triangle: A scalene triangle is the one whose all sides are unequal, i.e., have a distinct measure. As a result, all these sides are inclined at different angles to each other. Hence scalene triangles have sides and angles which have different measures.

- Isosceles Triangle: An isosceles triangle is the one whose two sides are equal and the angles opposite to the equal sides are equal in measure as well.

- Equilateral Triangle: An equilateral triangle is the one whose all three sides, as well as angles, measure equal. Since the angle sum property of a triangle states that the sum of all three angles of a triangle measures 180 degrees, each angle of an equilateral triangle measures 60 degrees.

- Right Triangle: A right triangle is the one whose all sides measure differently, with the two shorter sides being perpendicular to each other. The longest side is called the hypotenuse.

Perimeter of a Triangle
The perimeter of any enclosed space refers to the length around its sides. Summing up the length of all sides of a shape would yield its perimeter. Similarly, the perimeter of a triangle can be calculated by adding up the lengths of its three sides.
Perimeter of a regular triangle ABC = AB + BC + CA
The above formula can be further simplified for an equilateral triangle as follows:
Perimeter of an equilateral triangle with side a = a + a + a = 3a.
Area of a Triangle
The area of a triangle can be calculated in different ways depending upon the type of the triangle. These methods are as follows:
1. The area of a triangle can be calculated with the help of lengths of its base and altitude as follows:
Area of a triangle given its base and height = 1/2 × b × h
2. The above formula can be used for scalene, isosceles, and right triangles. But in the case of an equilateral triangle, the formula to calculate area is:
Area of an equilateral triangle with side a = 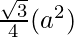
3. Sometimes, Heron’s formula has to be applied in order to calculate the area of a scalene triangle in the absence of any information regarding its angle measures and the length of its altitude.
Area of a triangle using Heron’s Formula = 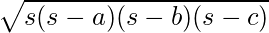 , where s is the semi-perimeter of the given triangle and a, b, c represent the lengths of the sides of the given triangle.
, where s is the semi-perimeter of the given triangle and a, b, c represent the lengths of the sides of the given triangle.
Sample Problems
Question 1. Find the perimeter and area of an equilateral triangle of side 6 cm.
Solution:
Perimeter of an equilateral triangle = 3a = 3(6) = 18 cm
Area of an equilateral triangle = 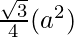 =
= 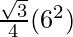
= 9√3 sq. cm
Hence, perimeter = 18 cm and area = 9√3 sq. cm.
Question 2. Find the perimeter of a right triangle whose base is 3 cm and hypotenuse measures 5 cm.
Solution:
As per Pythagoras Theorem, (hypotenuse)2 = (base)2 + (perpendicular)2
⇒ 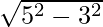 = perpendicular
= perpendicular
⇒ Perpendicular = 4 cm
So, perimeter of the triangle = 4 + 3 + 5 cm
= 12 cm
Hence perimeter of the given triangle is 12 cm.
Question 3. Find the area of a triangle whose base is 40 cm and altitude is 12 cm.
Solution:
Area of a triangle given its base and height = 1/2 × b × h
= 1/2 × 40 × 12
= 240 sq. cm
Thus, the area of the given triangle is 240 sq. cm.
Question 4. Find the side of an equilateral triangle whose perimeter is 75 cm.
Solution:
Perimeter of an equilateral triangle = 3a
3a = 75, or a = 25 cm
Hence the side of the triangle is 25 cm.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...