How to find the equation of an ellipse given the center and two points?

Question

GeeksforGeeks · Accepted Answer

A conic section can be defined as the set of points that describe the intersection of a right circular cone with a plane. The angle of intersection between the plane and the cone determines the shape of the conic section. When this angle is acute, that is, between 45° and 90°.

Alternatively, an ellipse can also be defined as such: a closed curve formed by a set of points whose sum of the distance from two fixed points is constant.

The standard equation of the ellipse whose center is (h, k) is,

$\dfrac{(x-h)^2}{a^2} + \dfrac{(y-k)^2}{b^2} = 1$

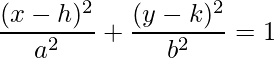
Question: Determine the equation of the standard form of the ellipse given: The coordinates of two points P (p, q) and M (m, n), and the coordinates of the center, O (h, k).

Solution:

It is known that the standard equation of the ellipse is,

$\dfrac{(x-h)^2}{a^2} + \dfrac{(y-k)^2}{b^2} = 1$

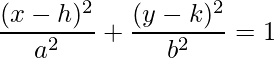
We have been provided the value of (h, k) in the question. Both P(p, q) and M(m, n) will satisfy the equation.

So, now we have two equations:

Equation 1: 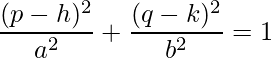$\dfrac{(p-h)^2}{a^2} + \dfrac{(q-k)^2}{b^2} = 1$

Equation 2: 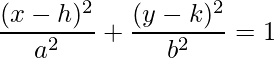$\dfrac{(x-h)^2}{a^2} + \dfrac{(y-k)^2}{b^2} = 1$

We can equate both the LHS of the equations (since the RHS is equal). Then, we get:

$\dfrac{(p-h)^2}{a^2} + \dfrac{(q-k)^2}{b^2} = \dfrac{(m-h)^2}{a^2} + \dfrac{(n-k)^2}{b^2}$

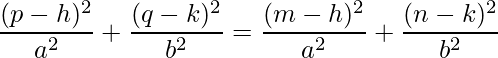
We can simplify this as:

$\dfrac{(p-h)^2 -(m-h)^2}{a^2} = \dfrac{(n-k)^2 - (q-k)^2}{b^2}$

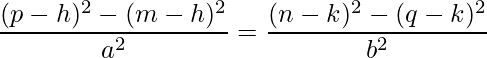
Using the formula a² – b² = (a – b)×(a + b), we can simplify the equation further:

$\dfrac {(p - m)\times(p + m - 2h)}{a ^ 2} = \dfrac {(n - q)\times(n +q- 2k)}{b^ 2}$

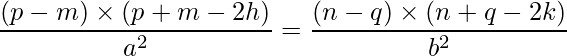
From this, we can get the relation between a and b as:

$a = b \times \sqrt \dfrac {(p - m)\times(p + m - 2h)}{(n - q)\times(n +q- 2k)}$

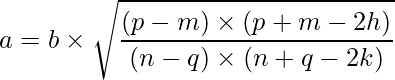
Now, we can plug this value in Equation 1 or Equation 2 to solve it finally.

Let us plug it into equation 1:

$\dfrac{(x-h)^2}{a^2} + \dfrac{(y-k)^2}{b^2} = 1$

$\dfrac{(p-h)^2}{ b^2 \times\dfrac {(p - m)×(p + m - 2h)}{(n - q)×(n +q- 2k)} } + \dfrac{(q-k)^2}{b^2} = 1$

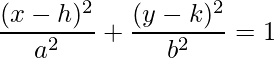
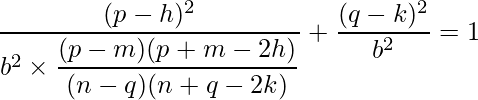
Finally, we can deduce that b is:

$b = \sqrt {\dfrac{(p-h)^2 \times (n - q)\times(n +q- 2k)}{(p - m)\times(p + m - 2h)} + (q-k)^2 }$

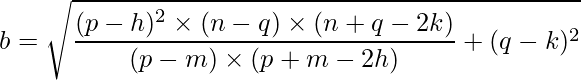
And hence, a is:

$a = \sqrt {\dfrac{(p-h)^2 (n - q)(n +q- 2k)}{(p - m)(p + m - 2h)} + (q-k)^2 } \times \sqrt \dfrac {(p - m)(p + m - 2h)}{(n - q)(n +q- 2k)}$

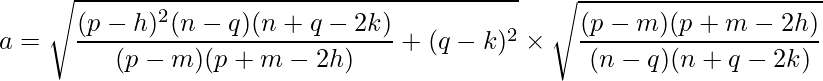
Given two points P (p, q) and M (m, n) of an ellipse with center (h, k), the equation of the ellipse in standard form is:

$\dfrac{(x-h)^2}{a^2} + \dfrac{(y-k)^2}{b^2} = 1$

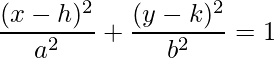
where,

$a = \sqrt {\dfrac{(p-h)^2 \times (n - q)\times(n +q- 2k)}{(p - m)\times(p + m - 2h)} + (q-k)^2 } \times \sqrt \dfrac {(p - m)\times(p + m - 2h)}{(n - q)\times(n +q- 2k)}$

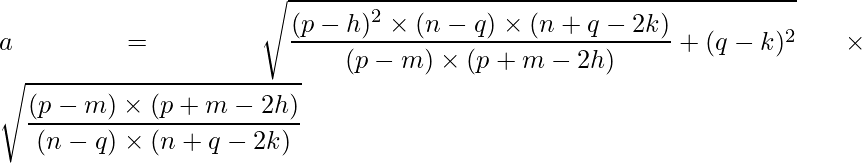
and

$b = \sqrt {\dfrac{(p-h)^2 \times (n - q)\times(n +q- 2k)}{(p - m)\times(p + m - 2h)} + (q-k)^2 }$

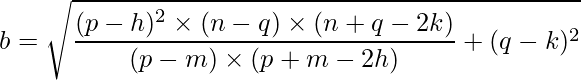
Sample Problems

Problem 1: Given that the center of an ellipse is (5, 2) and the points A (3, 4) and B (5, 6) pass through the ellipse, form the standard equation of the ellipse.

Solution:

Given that center of the ellipse is (h, k) = (5, 2) and (p, q) = (3, 4) and (m, n) = (5, 6) are two points on the ellipse.

We can use the values of a and b from the above formula to create the standard equation as:

$\dfrac{(x-h)^2}{a^2} + \dfrac{(y-k)^2}{b^2} = 1$

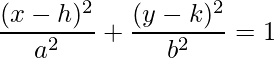
We know that,

$a = \sqrt {\dfrac{(p-h)^2 \times (n - q)\times(n +q- 2k)}{(p - m)\times(p + m - 2h)} + (q-k)^2 } \times \sqrt \dfrac {(p - m)\times(p + m - 2h)}{(n - q)\times(n +q- 2k)}$

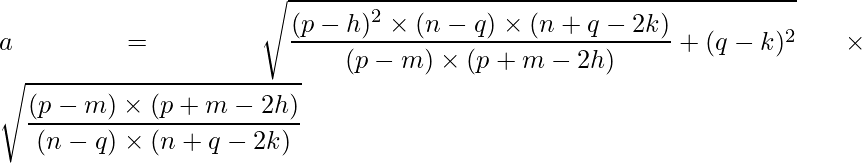
Substituting the values of p, q, h, k, m and n we get:

$\sqrt {\dfrac{(3-5)^2 \times (6 - 4)\times(6 +4- 22)}{(3 - 5)×(3 + 5 - 25)} + (4-2)^2 } \times \sqrt \dfrac {(3 - 5)\times(3 + 5 - 25)}{(6 - 4)×(6 +4- 22)}$

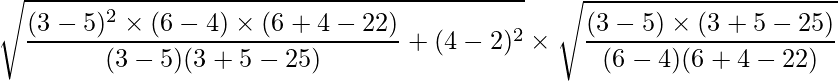
Solving, we get a ≈ 2.31.

Similarly, substituting the values of p, q, h, k, m and n in the formula for b, we get:

$\sqrt {\dfrac {(3-5)^2 \times (6 - 4)\times(6 +4- 22)}{(3 - 5)\times(3 + 5 - 25)} + (4-2)^2 }$

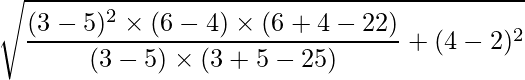
Solving, we get b = 4.

Therefore, the equation of the ellipse is:

$\dfrac{(x-5)^2}{5.33} + \dfrac{(y-2)^2}{16} = 1$

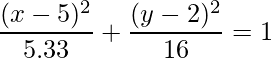
Problem 2: A hypothetical ellipse has its center at (5, 8). The points A (9, 2) and B (7, 6) pass through the ellipse. Is it possible for such an ellipse to exist in the real plane? Explain your answer.

Solution:

Our hypothesis is that the ellipse exists.

Given that center of the ellipse is (h, k) = (5, 8) and (p, q) = (9, 2) and (m, n) = (7, 6) are two points on the ellipse, we can use the values of a and b from the above formula to create the standard equation

$\dfrac{(x-h)^2}{a^2} + \dfrac{(y-k)^2}{b^2} = 1$

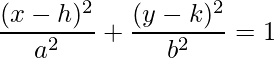
We know that,

$a = \sqrt {\dfrac{(p-h)^2 \times (n - q)\times(n +q- 2k)}{(p - m)\times(p + m - 2h)} + (q-k)^2 } \times \sqrt \dfrac {(p - m)\times(p + m - 2h)}{(n - q)\times(n +q- 2k)}$

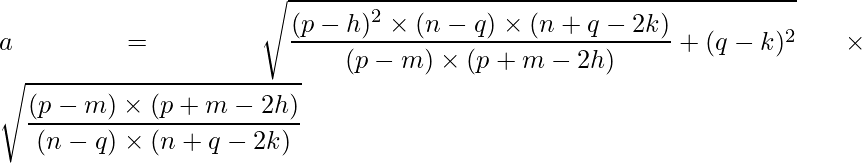
Substituting the values of p, q, h, k, m and n we get:

$a = \sqrt {\dfrac{(9-5)^2 \times (6 - 2)\times(6 +2- 28)}{(9 - 7)\times(9 + 7 - 25)} + (2-8)^2 } \times \sqrt \dfrac {(9 - 7)\times(9 + 7 - 25)}{(6 - 2)\times(6 +2- 28)}$

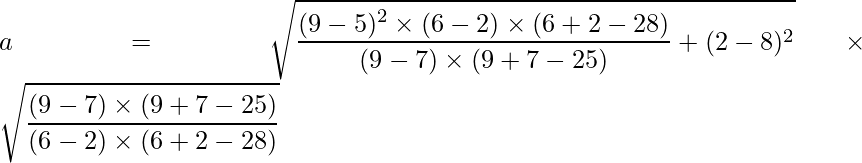
We cannot solve this and get a real value of a.

Therefore, our hypothesis is False. An ellipse with the given conditions cannot exist.

Problem 3: Given that the center of an ellipse is (1, 4) and the points A (2, 9) and B (12, 5) pass through the ellipse, form the standard equation of the ellipse.

Solution:

Given that center of the ellipse is (h, k) = (1, 4) and (p, q) = (2, 9) and (m, n) = (12, 5) are two points on the ellipse, we can use the values of a and b from the above formula to create the standard equation:

$\dfrac{(x-h)^2}{a^2} + \dfrac{(y-k)^2}{b^2} = 1$

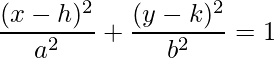
We know that,

$a=\sqrt {\dfrac{(p-h)^2 \times (n - q)\times(n +q- 2k)}{(p - m)\times(p + m - 2h)} + (q-k)^2 } \times \sqrt \dfrac {(p - m)\times(p + m - 2h)}{(n - q)\times(n +q- 2k)}$

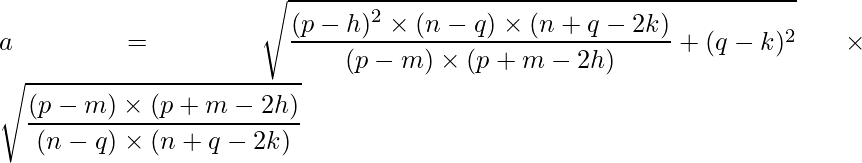
Substituting the values of p, q, h, k, m and n we get:

$a = \sqrt {\dfrac{(2-1)^2 \times (5 - 9)\times(5 +9- 24)}{(2 - 12)\times(2 + 12 - 21)} + (9-4)^2 } \times \sqrt \dfrac {(2 - 12)\times(2 + 12 - 21)}{(5 - 9)\times(5+9-24)}$

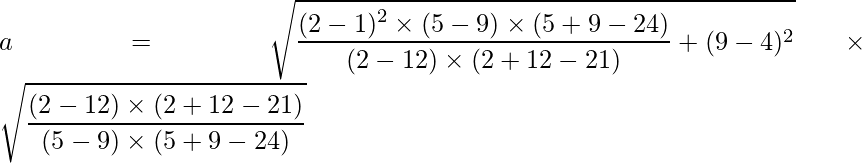
Solving, we get a ≈ 11.22.

Similarly, substituting the values of p, q, h, k, m and n in the formula for b, we get:

$b = \sqrt {\dfrac{(2-1)^2 (5 - 9)(5+9-24)}{(2 - 12)(2 + 12 - 21)} + (9-4)^2 }$

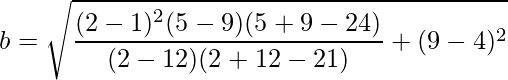
Solving, we get b ≈ 5.02.

Therefore, the equation of the ellipse is:

$\dfrac{(x-1)^2}{126} + \dfrac{(y-4)^2}{25.2} = 1$

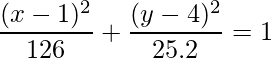
Problem 4: A hypothetical ellipse has its center at (1, 3). The points A (8, 2) and B (7, 5) pass through the ellipse. Is it possible for such an ellipse to exist in the real plane? Explain your answer.

Solution:

Our hypothesis is that the ellipse exists.

Given that center of the ellipse is (h, k) = (1, 3) and (p, q) = (8, 2) and (m, n) = (7, 5) are two points on the ellipse, we can use the values of a and b from the above formula to create the standard equation:

$\dfrac{(x-h)^2}{a^2} + \dfrac{(y-k)^2}{b^2} = 1$

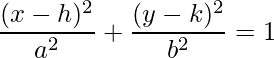
We know that,

$a = \sqrt {\dfrac{(p-h)^2(n - q)(n +q- 2k)}{(p - m)(p + m - 2h)} + (q-k)^2 }\times \sqrt \dfrac {(p - m)(p + m - 2h)}{(n - q)(n +q- 2k)}$

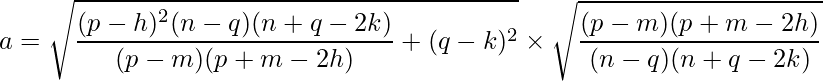
Substituting the values of p, q, h, k, m and n we get:

$a = \sqrt {\dfrac{(8-1)^2(5 - 2)(5 +2- 23)}{(8 - 7)(8 + 7 - 21)} + (2-3)^2 }\sqrt \frac {(8 - 7)(8 + 7 - 21)}{(5 - 2)(5 +2- 23)}$

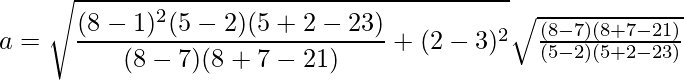
Solving this, we get a ≈ 7.3.

Similarly, substituting the values of p, q, h, k, m, and n in the formula for b, we get:

$b = \sqrt {\dfrac{(8-1)^2 (5 - 2)(5+2- 23)}{(8 - 7)(8+7-21)} + (2-3)^2 }$

Solving this, we get b ≈ 3.51.

As the values of a and b are real, our hypothesis is True. An ellipse that satisfies the given conditions can exist.

Problem 5: The center of an ellipse is at the Origin. The point (1, 5) lies on the ellipse. Does the point (11, 2) also lie on the ellipse?

Solution:

Our hypothesis is that an ellipse with a center at Origin (0, 0) passing through the points (11, 2) and (1, 5) exists.

Now, we can use the values of a and b from the above formula to create the standard equation

$\dfrac{(x-h)^2}{a^2} + \dfrac{(y-k)^2}{b^2} = 1$

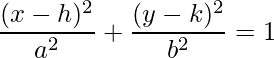
We know that,

$a = \sqrt {\dfrac{(p-h)^2 (n - q)(n +q- 2k)}{(p - m)(p + m - 2h)} + (q-k)^2 } \sqrt \dfrac {(p - m)(p + m - 2h)}{(n - q)(n +q- 2k)}$

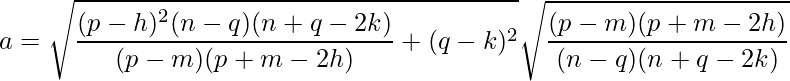
Substituting the values of p, q, h, k, m and n we get:

$a = \sqrt {\dfrac{(11-0)^2 (5 - 2) (5 +2- 20)}{(11 - 1) (11 + 1 - 20)} + (2-0)^2 } \times \sqrt \dfrac {(11 - 1)(11 + 1 - 20)}{(5 - 2)(5 +2- 20)}$

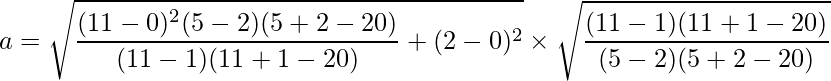
Solving this, we get a ≈ 11.99.

Similarly, substituting the values of p, q, h, k, m and n in the formula for b, we get:

$b = \sqrt {\dfrac{(11-0)^2 (5 - 2)(5 +2- 20)}{(11 - 1)(11 + 1 - 20)} + (2-0)^2 }$

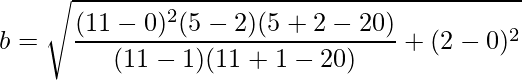
Solving this, we get b ≈ 5.02.

As the values of a and b are real, our hypothesis is True. The point (11, 2) does lie on the ellipse.

Suggest improvement

Share your thoughts in the comments

How to find the equation of an ellipse given the center and two points?

Question: Determine the equation of the standard form of the ellipse given: The coordinates of two points P (p, q) and M (m, n), and the coordinates of the center, O (h, k).

Solution:

Sample Problems

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?