How to find square roots without a calculator?
Last Updated :
09 Nov, 2023
The number system is the system defined for the different numbers and the way they could be arranged. There are many types of number systems but mostly 4 types are well known. They are Binary number systems, Decimal number systems, Octal number systems, and Hexadecimal number systems. The decimal number system is mostly used in mathematics, it involves numbers from 0-9. There are multiple operations done on the numbers, for example, finding squares and square roots of numbers, lets learn in detail about the square roots of the numbers,
Square root
The square root of a number is a value which when multiplied with itself gives the original number. For example, the square root of 9 is 3, when 3 is multiplied by itself, the original number obtained is 9. The symbol that denotes square root in mathematics is √.
This symbol (√) is called radical and the number inside the radical symbol is known as radicand. The number or the value present inside the root symbol might be a perfect square or an imperfect square. For example- 4 is a perfect square whereas 3 is an imperfect square. So, based on the nature of value inside the root, the final answer or the square root may be a natural number of a decimal number.
Now let’s find out how to calculate the square root of different numbers.
Square roots without a calculator
As above defined, the square root of a number is the value which when multiplied with itself will provide the original number only. There are three ways to find square root without a calculator
Prime factorization
This is a long but simple method to find the square root of any number. Prime factorization involves finding factors of that number and then pairing the common numbers in a pair of two. finally, taking the square roots of the prime factors. Let’s see an example of this,
Question: find the square root of 484
Solution:
484=2 × 2 × 11 × 11
So, √484= √(2 × 2 × 11 × 11) = 2 × 11 =22
Guess & Check method
This method is used to give the approximate value of any number. The guess method saves time as it gives an approximate range of values between which the root exists. it is more efficient when the number inside the root is an imperfect number. Let’s see an example of this,
Question: find the square root of 20.
Solution:
Start guess and check method by noting that since √16 = 4 and √25 = 5, then √20 must be between 4 and 5. As second step, in order to reach nearer to the actual answer, lets take a number between 4 and 5. lets assume it to be 4.5. Lets do square of 4.5 which comes out to be 20.25, which is greater than 20, therefore the root must be smaller than 4.5, lets choose 4.4, square of 4.4 is 19.36. thus, the most approx and accurate root of 20 is 4.4
Long division method
It is a very easy way to get the square root of imperfect squares. The long division method is mostly preferred over the other methods since it provides an accurate answer. Let’s understand this algorithm using an example,
Question: find the square root of 627
Solution:
Step 1 Group the numbers in pairs from right to left ,leaving one or two digit in left (here its 6).

Step 2 Think of a number whose square is less than the first number (6), its 2, So,write it like this –
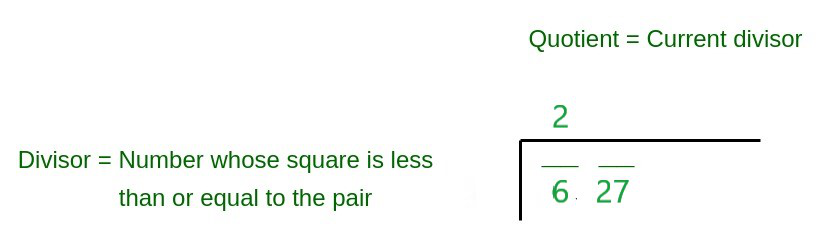
Step 3 Is to square the number 2 and write the result beneath 6 and then subtract as shown below,

Step 4 Multiply the quotient by 2 and and write it down in parenthesis with an empty line next to it as shown below,

Step 5 Now find out the number which when multiplied by forty something would be lesser than 225. Lets guess 5. then 45×5=225, which is less than 227, So write it as shown below-
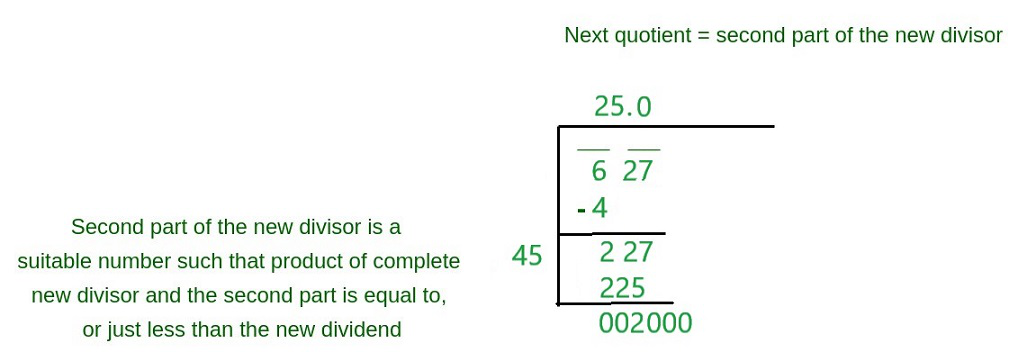
Step 6 Then repeating step 4, multiply the quotient with 2 write it down in parenthesis with an empty line next to it as shown below,

Step 7 Repeating step 5, find out the number which when multiplied by five hundred something would be lesser than 2000. Lets guess 5, then 505×5=2525, which is bigger than 2000, lets guess 4, then 504×3=1512. So write it as shown below,
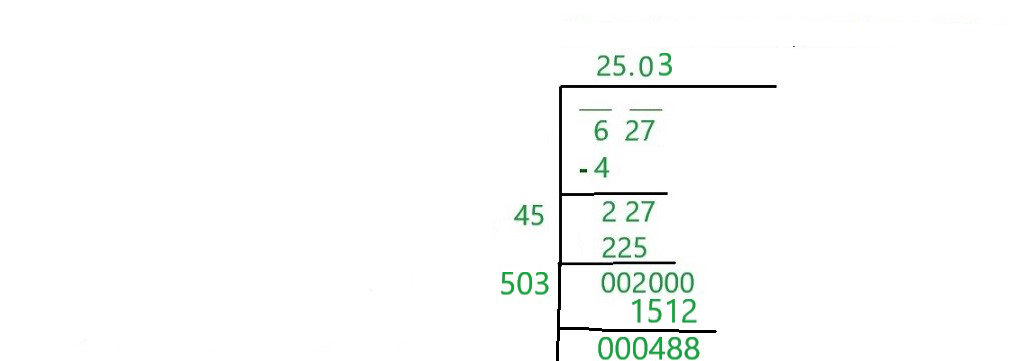
The square root of 627 with two decimal place is 25.03, which is accurate.
Sample Problems
Question 1: Find the square root of 144
Solution:
144=2 × 2 × 2 × 2 × 3 × 3
So √144= √(2 × 2 × 2 × 2 × 3 × 3) = 2 × 2 × 3 =12
Question 2: Find the square root of 169
Solution:
169=13 × 13
So √169 = √(13 × 13) = 13
Question 3: Find the square root of 6 by the Guess and check method.
Solution:
Start guess and check the method by noting that since √9 =3 and √4 = 2, then √6 must be between 2 and 3. As the second step, in order to reach nearer to the actual answer, let’s take a number between 2 and 3. Let’s assume it to be 2.5. Let’s do a square of 2.5 which comes out to be 6.25, which is greater than 6. therefore the root must be smaller than 2.5. Let’s choose 2.4, square of 2.4 is 15.76. Thus, the most approx and accurate root of 6 is 2.4
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...