How to create a random Graph in C++?
Last Updated :
25 Nov, 2022
A graph is a type of non-linear data structure that has two types of components “Vertices” (nodes) and “edges”. It contains a set of vertices (V) and a set of edges (E). Two nodes of the graph are connected by an edge. A graph is denoted by G(V, E).
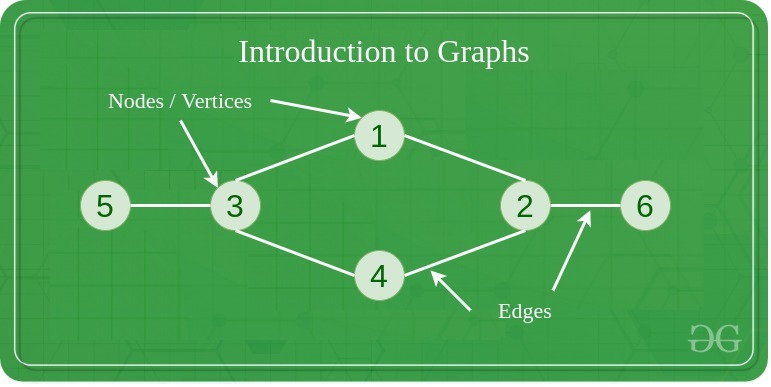
Example of a Graph
Ways to represent a Graph:
There are two major ways of representing a Graph in C++:
- Adjacency Matrix
- Adjacency List
The other way of representing the graph may include Incidence Matrix and Incidence List. The way to represent the graph we use is based on our requirements.
Adjacency Matrix:
The graph is represented in the form of a Matrix. It is a V * V matrix, where V represents the number of vertices present in the graph.
Let us take a matrix as adj[][]. If there is any value in the cell adj[i][j], it represents that there is an edge from i to j. The adjacency matrix for an undirected graph is always symmetric. It can be used to represent the weighted graph and unweighted graph. In an unweighted graph adj[i][j] = 1 but in a weighted graph adj[i][j] is equal to the weight of the edge.

Example of an adjacency matrix
Adjacency List:
It is also a common method of representing the graph. Let the list be array[]. An entry array[i] represents the list of vertices that are adjacent to the ith vertex. It can also be used to represent a weighted graph. When it is being used to represent a weighted graph then the weights of edges can be represented as lists of pairs.

Example of adjacency list
Generate a random Graph using an Adjacency Matrix:
Follow the below steps to implement:
- We create a function named GenRandomGraphs and pass a variable to it. (the variable is the number of edges and vertices)
- Generate random edges till all the possible edges are covered.
- For each edge generated, check if this edge was previously generated or if both ends of the edge are the same.
- After this, traverse for each vertex:
- Find out the edges for which the current vertex is an end node.
- Insert that in the adjacency list for the current vertex.
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
void GenRandomGraphs(int NOEdge, int NOVertex)
{
int i, j, edge[NOEdge][2], count;
i = 0;
while (i < NOEdge) {
edge[i][0] = rand() % NOVertex + 1;
edge[i][1] = rand() % NOVertex + 1;
if (edge[i][0] == edge[i][1])
continue;
else {
for (j = 0; j < i; j++) {
if ((edge[i][0] == edge[j][0]
&& edge[i][1] == edge[j][1])
|| (edge[i][0] == edge[j][1]
&& edge[i][1] == edge[j][0]))
i--;
}
}
i++;
}
cout << "The generated random graph is: " << endl;
for (i = 0; i < NOVertex; i++) {
count = 0;
cout << "\t" << i + 1 << "-> { ";
for (j = 0; j < NOEdge; j++) {
if (edge[j][0] == i + 1) {
cout << edge[j][1] << " ";
count++;
}
else if (edge[j][1] == i + 1) {
cout << edge[j][0] << " ";
count++;
}
else if (j == NOEdge - 1 && count == 0)
cout << "Isolated Vertex!";
}
cout << " }" << endl;
}
}
int main()
{
int i, e, n;
cout << "Random graph generation: " << endl;
n = 7 + rand() % 6;
cout << "The graph has " << n << " vertices" << endl;
e = rand() % ((n * (n - 1)) / 2);
cout << "and has " << e << " edges." << endl;
GenRandomGraphs(e, n);
return 0;
}
|
Output
Random graph generation:
The graph has 8 vertices
and has 18 edges.
The generated random graph is:
1-> { 5 4 2 }
2-> { 4 8 6 3 1 5 }
3-> { 5 4 7 2 }
4-> { 2 3 7 1 8 5 }
5-> { 3 1 7 4 2 8 }
6-> { 2 8 7 }
7-> { 4 3 5 6 }
8-> { 2 6 4 5 }
Time Complexity: O(E2 + E*V) where E is the number of edges and V is the number of vertices
Auxiliary Space: O(V2)
Related Articles:
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...