How to convert from AC to DC?

INTRODUCTION:

Electricity is a branch of physics that concerns the properties and movement of electrically charged particles. When charged particles are on the surface of a material, it is called static electricity. The movement of electrical charges creates magnetic fields, while changes in magnetic fields can create electricity. Electricity flows from higher potential to lower potential. Electricity and magnetism are related to each other. Thus, the study of electric fields and magnetic fields together is known as electromagnetism.

Alternating Current (AC)

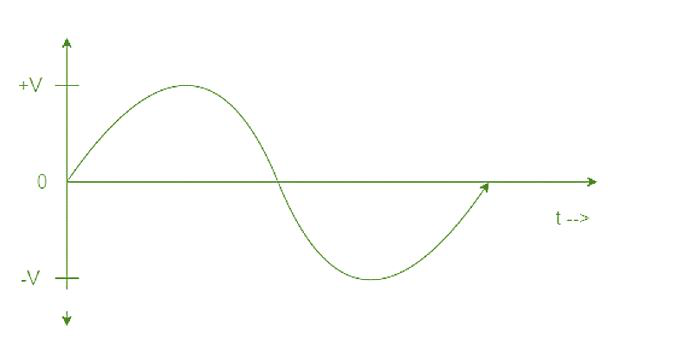
Alternating current (AC) is the flow of electric charge that periodically reverses. It starts, say, from zero, grows to a maximum, decreases to zero, reverses, reaches a maximum in the opposite direction, returns again to the original value, and repeats this cycle indefinitely. The interval of time between the attainment of a definite value on two successive cycles is called the period; the number of cycles or periods per second is the frequency; and the maximum value in either direction is the amplitude of the alternating current.

Direct Current (DC)

Direct current (DC) is the one-directional flow of electric charge. An electrochemical cell is a prime example of DC power. Direct current may flow through a conductor, such as a wire, but it can also flow through semiconductors, insulators, or even through a vacuum, as in electron or ion beams. The electric current flows in a constant direction.

AC and DC circuits

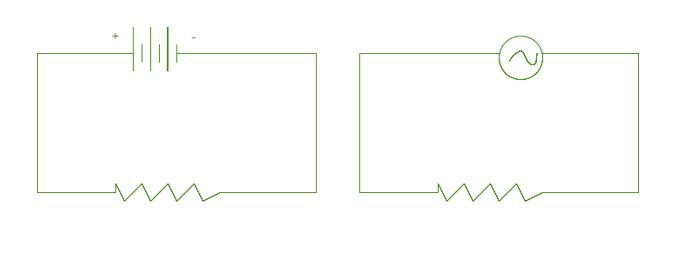
In the DC circuit, a DC supply is provided, so a steady amount of current flows every time, whereas in the AC circuit, an AC supply is provided, so polarity changes at every moment. An AC circuit has two cycles: a positive cycle and a negative cycle. Each second, polarity changes many times based on the frequency of supply given in hertz.

Representation of AC

A sinusoidal alternating current can be represented by the equation i = I sin ωt, where i is the current at time t and I is the maximum current. In a similar way, we can write for a sinusoidal alternating voltage,

v = V sin ωt

Where v is the voltage at time t and V is the maximum voltage.

Where, ω = 2πƒ

ƒ = frequency

t = time period

When do you need to convert dc to ac power?

You need to convert DC to AC power in a variety of situations such as

• Renewable Energy Systems
• Electric Vehicles
• Uninterruptible Power Supplies (UPS)
• Home and Office Appliances

What is the easiest way to convert AC to DC?

The simplest and most effective means of converting Alternating Current (AC) to Direct Current (DC) is through a circuit component called a rectifier. Rectifiers are typically constructed from diodes, which allow current to flow only in a single direction. In a simple setup called a half wave rectifier, diodes can block the negative part of the AC waveform, producing a pulsating DC output. To obtain a smoother DC signal, a full wave rectifier is used, which converts the negative half of the AC waveform into a positive. Finally, capacitors are included in this setup to filter the output and decrease its ripple, resulting in a more consistent DC signal.

lets take example of How Phone chargers convert AC to DC ?

Phone chargers use a part known as a transformer ,In order to reduce the high-voltage AC from the main supply to a level that is safer. Following that, a rectifier circuit is used to convert this lower voltage AC to DC. Diodes in the circuit permit current to flow only in one way. The rectifier in a phone charger functions similarly to a basic rectifier in that it suppresses the negative half of the AC waveform while simultaneously flipping the positive half into positive, producing a pulsing DC output. Capacitors are used as a filter to lessen ripple and improve the output’s consistency and smoothness. The phone is powered on or charged using this filtered DC output.

Need of conversion from AC to DC

As we have seen AC and DC currents,. It should be noted that depending on the device, different types of supply are provided. The supply that comes to households in India is a 220V AC supply. But our mobile chargers, adapters, and various other devices work on DC power. So, there should be methods to interconvert these supplies so that we can use the necessary supply whenever we need it.

Conversion from AC to DC

1. Rectification: Rectification is the process of converting AC to pulsating DC. It involves using diodes to allow current to flow in only one direction.

• There are two main types of rectifiers:

• Half-Wave Rectification: In this method, only one half of the AC waveform is allowed to pass through, resulting in a DC output with a significant amount of ripple.
• Full-Wave Rectification: This method utilizes either a bridge rectifier or a center-tapped transformer along with diodes to convert both halves of the AC waveform into DC, resulting in a smoother output with less ripple.

2. Inverters and Converters: In some cases, AC can be converted to DC by first converting it to a different form of AC using an inverter and then rectifying the AC output to obtain DC. This approach is common in renewable energy systems, where DC power from sources such as solar panels or wind turbines is converted to AC for use in the electrical grid.

Covert AC to DC

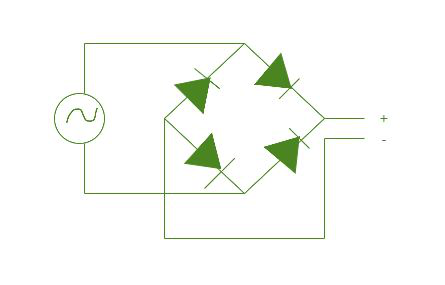
After stepping down the voltage, AC is converted to DC using rectifiers. A full-bridge rectifier can be used to convert AC to DC. In this device, 4 diodes are used, which operate in forward bias and not reverse bias. During the positive half cycle, two of the diodes are operated, and during the negative half cycle, the other two diodes are operated. This way, the AC supply is rectified to the DC supply. The below image is of a full-bridge rectifier circuit used to convert AC to DC.

Purifying DC waveforms

The DC waveforms generated in the above step do not have pure DC waveforms. It is in the form of pulses and has a fluctuating supply. Capacitors are devices that are used to do this task. The capacitor is used to store energy when the input voltage is increasing from zero to the highest value. The energy from the capacitor can be discharged when the input voltage decreases to zero. This straightens the waveforms to a good extent.

Fixing up DC voltage

Finally, DC voltage is converted to the fixed desired value by using the voltage regulator IC. The DC voltage regulator IC consists of an integrated circuit that finally converts our DC supply to a given voltage. For example, to convert to a 5V DC supply, we use the 7805 Voltage Regulator IC. And to convert to a 9V DC supply, we use a 7809 voltage regulator IC.

• Rotary Converter

A rotary converter is basically a mechanical rectifier, inverter, or frequency converter. It converts alternating current (AC) to direct current (DC) using mechanical energy. The rotary converter consists of two machines attached to a single rotating armature and a set of field coils. It has a DC generator (dynamo) with an evenly spaced set of slip rings tapped into its rotor windings. The alternating current is rectified using a commutator, from which direct current is extracted from the rotor. The energized coils rotate and excite the stationary field windings; this produces direct current. The rotary converter acts as a hybrid dynamo and mechanical rectifier. It also acts as an alternator due to AC slip rings.

• Switched-mode power supply (SMPS)

A switched-mode power supply (SMPS) is an electronic circuit that consists of switching devices such as MOSFETs that are turned on and off at high frequencies (in kHz) and storage components such as inductors or capacitors, which are used to supply power when the switching device is in its non-conduction state. These devices are connected using a complex circuit and used to convert AC to DC.

Applications of AC-to-DC converters

• They are used in vacuum cleaners, washing machines, and refrigerators.
• Appliances such as computers, televisions, cell phone chargers, etc. work on DC. So, AC-to-DC converters play a very important role in these devices.
• They are also used in medical equipment, factory automation, and process control systems.
• The other applications of AC to DC converters are in renewable energy management, test & measuring equipment, aerospace, and transportation systems.

Conclusion

Knowing the differences between DC and AC power is essential as our reliance on modern devices and appliances grows. By Skillfully balancing the unique attributes of these two electrical powerhouses’ distinct qualities, improved performance and energy efficiency can be unlocked. Energize your innovations, change your lifestyle, and maintain a seamless connection to the digital world by utilizing the power of energy.

Sample Problems

Problem 1: A 200 mH coil is connected to an AC circuit with a 5 mA current. If the frequency is 2000 Hz then find out the voltage.Hz,

Solution: 

Given: L = 200 × 10^-3 H

I = 5 × 10^-3 A

f = 2000 Hz

We know that Inductive Reactance, X_L = L × ω = L × 2πƒ

= 2 × 3.14 × 2000 × 0.2

= 2512 Ohm

V = I X_L 

= 0.005 × 2512

= 12.56 V

So, the voltage is 12.56 V

Problem 2: Find the instantaneous value of alternating voltage v = 5 sin(2π ×10⁴ t) volt at:

1. 0 s 
2. 20 μs 
3. 40 μs.

Solution:

At t = 0 s,

v = 5 sin(0) = 0 V

At t = 20 μs,

v = 5 sin(2π ×10⁴ × 20 × 10^-6) 

= 5 sin( 40π × 10^-2 )

= 5 sin(1.25)

= 5 × 0.94

= 4.74 V

At t = 40 μs,

v = 5 sin(2π ×10⁴ × 40 × 10^-6)

= 5 sin( 80π × 10^-2 )

= 5 sin(2.5)

= 5 × 0.59

= 3 V

So, the instantaneous value of alternating voltage at 0 s, 20 μs, 40 μs is 0V, 4.74V, 3V respectively.

Problem 3: The current across an inductive coil is given by 0.7 sin (300t – 40°) A. Write the equation for the voltage if the inductance is 60 mH.

Solution:

L = 60 × 10^-3 H, i = 0.7 sin (300t – 40°) A

X_L = ωL = 300 × 60 × 10^-3 = 18 Ω

V_m = I_m XL = 0.7 × 18 = 12.6 V

In an inductive circuit, the voltage leads the current by 90° Therefore,

v = V_m sin ( ωt + 90°)

v = 12.6 sin(300t −40 + 90°)

v = 12.6 sin(300t +50º) V

So, the equation for voltage is v = 12.6 sin(300t +50°).

Problem 4: If the equation for an alternating current is given by i = 45 sin 314t. Then find the peak value, frequency, time period, and instantaneous value at t = 1 ms.

Solution:

i = 45 sin 314t; t = 1 ms = 1 × 10^-3 s

Comparing with the general equation of an alternating current, i = I_m sin ωt.

• Peak value, I_m = 45 A
• Frequency, f = ω/2π = 314 / 2 × 3.14 = 50 Hz
• Time period, T = 1/f = 150 = 0 .02 s

At t = 2 ms,

Instantaneous value,

i = 45sin(3.14 × 1 × 10⁻³)

i = 0.14 A

Problem 5: If the DC voltage of the supply is 5V and the current is 2.5 A. Then find the resistance in the circuit.

Solution:

R = V/I

= 5/2.5

= 2 Ohm.

So, the resistance in the circuit is 2 Ohm.

Problem 6: Write down the equation for a sinusoidal voltage of 30 Hz and its peak value is 50V. Also, find time for one cycle.

Solution:

f = 30 Hz, V_m = 50V

v = V_m sinωt

= V_m sin2πft

= 50 sin(2π × 30)t

= 50 sin(60 × 3.14)t

v = 50 sin188t 

T = 1 / f 

= 1 / 30

= 0.033 sec

= 33 ms.

So, equation is v = 50 sin188t and time for one cycle 33 ms.

Frequently Asked Questions

What is AC and DC?

AC stands for alternating current, where the flow of electric charge periodically reverses direction. DC stands for direct current, where the flow of electric charge is constant in one direction.

What is the difference between AC and DC?

AC changes direction periodically, typically used in household electricity and power grids. DC flows in one direction continuously, commonly used in batteries, electronics, and many low-voltage applications.

How is AC converted to DC?

AC to DC conversion is achieved using devices called rectifiers. These devices convert the alternating voltage of AC into a constant voltage of DC. Rectifiers can be diode-based (half-wave or full-wave) or semiconductor-based (such as bridge rectifiers).

What are the applications of AC to DC conversion?

AC to DC conversion is essential for powering electronic devices, such as computers, TVs, smartphones, and household appliances. It is also used in power supplies for industrial machinery, transportation systems, and renewable energy systems.

What are the advantages of DC over AC?

DC has advantages in certain applications, such as electronic devices and electric vehicles, due to its ability to provide stable voltage and efficient power transmission over long distances. DC systems are also easier to control and integrate with renewable energy sources.

How does AC to DC conversion impact efficiency?

AC to DC conversion can result in energy losses due to conversion inefficiencies, heat generation, and power factor issues. However, advancements in power electronics technology have improved conversion efficiency, making AC to DC conversion more energy-efficient for many application