How to Compute a Discrete-Fourier Transform Coefficients Directly in Java?

The Discrete Fourier Transform (DFT) generally varies from 0 to 360. There are basically N-sample DFT, where N is the number of samples. It ranges from n=0 to N-1. We can get the co-efficient by getting the cosine term which is the real part and the sine term which is the imaginary part. 

The formula of DFT:

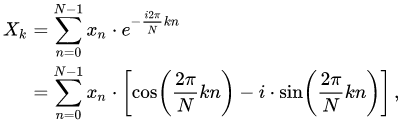
Example :

Input:

Enter the values of simple linear equation
ax+by=c
3
4
5
Enter the k DFT value
2


Output:

(-35.00000000000003) - (-48.17336721649107i)

Input:

Enter the values of simple linear equation
ax+by=c
2
4
5
Enter the k DFT value
4

Output:

(-30.00000000000001) - (-9.747590886987172i)

Approach:

• First, let us declare the value of N is 10
• We know the formula of DFT sequence is X(k)= e^jw ranges from 0 to N-1
• Now we first take the inputs of a, b, c, and then we try to calculate in “ax+by=c” linear form
• We try to take the function in an array called ‘newvar’.

newvar[i] = (((a*(double)i) + (b*(double)i)) -c);

• Now let us take the input variable k, and also declare sin and cosine arrays so that we can calculate real and imaginary parts separately.

cos[i]=Math.cos((2*i*k*Math.PI)/N);

sin[i]=Math.sin((2*i*k*Math.PI)/N);

• Now let us take real and imaginary variables
• Calculating imaginary variables and real variables like

real+=newvar[i]*cos[i];

img+=newvar[i]*sin[i];

• Now we will print this output in a+ ib form

Implementation:

Java

// Java program  to Compute a Discrete-Fourier
// Transform Coefficients Directly

import java.io.*;
import java.util.Scanner;

class GFG {

    public static void main(String[] args)
    {

        // Size of the N value
        int N = 10;

        // Enter the values of simple linear equation
        System.out.println(
            "Enter the values of simple linear equation");
        System.out.println("ax+by=c");

        // We declare them in data_type double..
        double a = 3.0;
        double b = 4.0;
        double c = 5.0;

        // Here newvar function array is declared in size
        // N..
        double[] newvar = new double[N];

        // Now let us loop it over N and take the function
        // Now the newvar array will calculate the function
        // ax+by=c for N times

        for (int i = 0; i < N; i++) {
            // This is the way we write that,
            // We are taking array A as of 'a'x
            // array B as of 'b'y
            newvar[i]
                = (((a * (double)i) + (b * (double)i)) - c);
        }

        System.out.println("Enter the k DFT value");

        // Here we declare the variable k
        int k = 2;

        // Here we take 2 terms cos and sin arrays
        // which will be useful to calculate the real and
        // imaginary part The size of both arrays will be 10

        double[] cos = new double[N];
        double[] sin = new double[N];

        // Iterating it to N
        // Now let us calculate the formula of cos and sin

        for (int i = 0; i < N; i++) {

            // Here cos term is real part which is
            // multiplied into 2ikpie/N
            cos[i] = Math.cos((2 * i * k * Math.PI) / N);

            // Here sin term is imaginary part which is also
            // multiplied into 2ikpie/N
            sin[i] = Math.sin((2 * i * k * Math.PI) / N);
        }

        // Now to know the value of real and imaginary terms
        // First we declare their respective variables
        double real = 0, img = 0;

        // Now let us iterate it till N

        for (int i = 0; i < N; i++) {

            // real part  can be calculated by adding it
            // with newvar and multiplying it with cosine
            // array
            real += newvar[i] * cos[i];

            // Imaginary part is calculated by adding it
            // with newvar and multiplying it with sine
            // array
            img += newvar[i] * sin[i];
        }

        // Now real and imaginary part can be written in
        // this equation form
        System.out.println("(" + real + ") - "
                           + "(" + img + "i)");
    }
}

Output

Enter the values of simple linear equation
ax+by=c
Enter the k DFT value
(-35.00000000000003) - (-48.17336721649107i)

Time complexity: O(n)

Auxiliary space: O(n) for array