All electromagnetic radiation is light, and it occurs over an extremely wide range of wavelengths, from high-energy gamma waves with shorter wavelengths to low-energy radio waves with longer wavelengths. But the human eye can detect only a small portion of the radiation, and that portion is referred to as visible light.
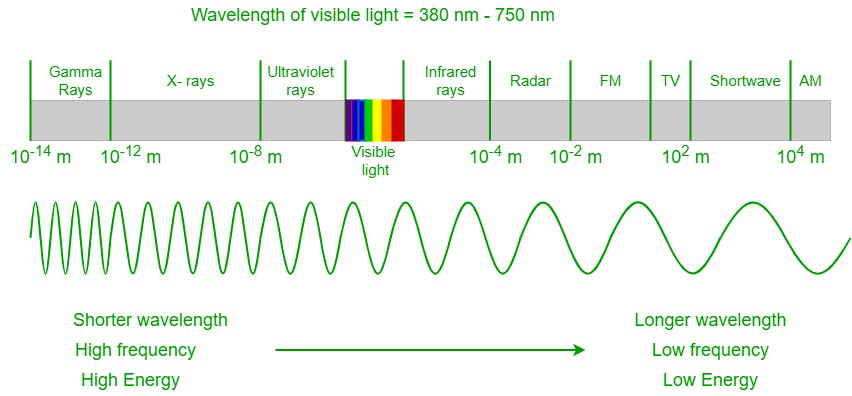
Electromagnetic spectrum
When a visible spectrum travels through a prism, the light gets separated into a spectrum of colors of different wavelengths. Our eyes can detect the outer-most layer of the sun, the corona, in visible light.
How is the Wavelength of Light Calculated?
As light has the properties of a wave and a particle, it can be expressed in two equations:
The velocity possessed by light is given as
V = λf
The energy possessed by light is given as
E = hf
Where,
- ν is the velocity of the light.
- λ is the wavelength of the light.
- f is the frequency of the light.
- E is the energy of the light wave.
- h is the Planck’s Constant ( 6.64 × 10-34 joule.second)
Wavelength
A wavelength is one of the properties of a wave and is defined as the distance between the two successive crests or troughs of a wave, where a crest is the highest point of the wave, and a trough is the lowest point of the wave. Since wavelength is a distance or length between two points, it is measured in meters, centimeters, millimeters, micrometers, etc. It is denoted by the symbol Lambda ‘λ’.

Wave
Frequency
Frequency (f) is defined as the total number of wave cycles or oscillations produced per unit of time. Frequency is measured in terms of Hertz (Hz) or s-1.
The formula for the frequency:
Frequency (f) = 1/period(T)
f = 1/T
- A period is defined as the time taken to complete an oscillation.
- From the equation of frequency, we can conclude that the frequency of a wave is inversely proportional to its period.
- 1 Hertz = 1 oscillation/second
Wave velocity
The velocity of a wave or wave velocity is defined as the distance traveled by the wave in a unit of time. The S.I. unit of wave velocity is ms-1.
- Light travels with a speed in the vacuum of 29,97,92,458 m/s, i.e., approximately 3 × 108 m/s, and it is represented by the symbol c.
Wavelength of the light
The wavelength of light refers to the distance between successive peaks or troughs in a wave of light. It’s commonly measured in units such as nanometers (nm) or meters (m). The wavelength of light determines its color, with shorter wavelengths corresponding to colors like blue and violet, and longer wavelengths corresponding to colors like red and orange.
Here are some approximate ranges for the visible spectrum:
- Red light: 620 nm to 750 nm
- Orange light: 590 nm to 620 nm
- Yellow light: 570 nm to 590 nm
- Green light: 495 nm to 570 nm
- Blue light: 450 nm to 495 nm
- Violet light: 380 nm to 450 nm
We know that light possesses the characteristics of both a wave and a particle. So, the wavelength of a light wave is given as;
λ = c/f
Where λ is the wavelength of light
c is the velocity of light and
f is the frequency of the light
The energy of a photon is given as,
E = h × f =
Where E is the energy of a photon
h is the Planck’s constant i.e., h = 6.64 × 10-34 joule-second
Wavelength, Frequency, and Energy of the visible light spectrum
| Color | Wavelength | Frequency | The energy of a photon |
| Violet | 380 – 450 nm | 668-789 THz | 2.75 – 3.26 eV
|
| Blue | 450-495 nm | 606-668 THz | 2.50 – 2.75 eV
|
| Green | 495-570 nm | 526-606 THz | 2.17 – 2.50 eV
|
Yellow
| 570-590 nm | 508-526 THz | 2.10 – 2.17 eV
|
Orange
| 590-620 nm | 484-508 THz | 2.00 – 2.10 eV
|
Red
| 620-750 nm | 400-484 THz | 1.65 – 2.00 eV
|
Sample Problems
Problem 1: Calculate the wavelength of the visible light with a frequency of 5.36 × 1014 Hz.
Solution:
Given the frequency of light = 5.36 × 1014 Hz
We know, that the velocity of light (c) = 3 × 108 m/s
Now, the wavelength of light (λ) = 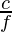
⇒ λ =
⇒ λ = 5.60 × 10-7 m
Hence, the wavelength is 5.60 × 10-7 m
Problem 2: If a microwave oven emits microwave energy of 1.64 × 10-24 J, then calculate the wavelength of the microwave emitted.
Solution:
Given data,
The energy of microwave emitted = 1.64 × 10-24 J
We know, that the energy of a photon =
h = 6.64 × 10-34 joule-second
⇒ 1.64 × 10-24 = 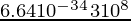
⇒ λ = 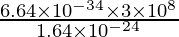
⇒ λ = 12.146 × 10-2 m = 12.15 cm
Hence, the wavelength of the microwave emitted is 12.15 cm.
Problem 3: If a radio station broadcasts at a frequency of 555 kHz, then calculate the wavelength of radio waves emitted.
Solution:
Given,
Frequency of radio waves = 555 KHz
We know, that the velocity of light (c) = 3 × 108 m/s
Now, the wavelength of light (λ) = 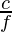
⇒ λ =
⇒ λ = 540 m
Hence the wavelength of radio waves emitted is 540 m.
Problem 4: Calculate the wavelength of yellow light emitted from a sodium lamp at a frequency of 5.15 × 1014 Hz.
Solution:
Given,
The frequency of yellow light = 5.15 × 1014 Hz
We know, that the velocity of light (c) = 3 × 108 m/s
Now, the wavelength of light (λ) =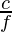
⇒ λ =
⇒ λ = 582.5 × 10-9 m = 582.5 nm
Hence, the wavelength of the yellow light is 582.5 nm.
Problem 5: Calculate the wavelength of a photon with an energy of 3.35 × 10-19 Joules.
Solution:
Given,
The energy of a photon = 3.35 × 10-19 Joules.
We know, that the energy of a photon =
h = 6.64 × 10-34 joule-second
⇒ 3.35 × 10-19 =
⇒ λ = 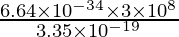
⇒ λ= 5.94 × 10-7 m = 594 nm
Hence, the wavelength of the photon is 594 nm.
Problem 6: The broadcasting frequency of a radio station is 101 MHz. What will be the wavelength of the wave if the broadcast wave is an electromagnetic wave?
Solution:
Given data, Frequency of the wave = 101 MHz = 101 × 106 Hz
Speed of light = 3 × 108 m/s
Now, the wavelength of light (λ) = c/f
⇒ λ = (3 × 108)/(101 × 106)
⇒ λ = 2.97 m
Hence, the wavelength of the broadcast wave is 2.97m
Frequently Asked Questions
What happens when a light beam moves from one medium to another in terms of frequency?
While a light beam is moving from one medium to another, its frequency stays constant.
What characteristics do the light waves that the laser emits have?
The characteristics of the light waves that the laser emits are as follows:
- Their phases are identical.
- Their amplitudes are same.
- Their frequencies are same.
Why does glass allow light to move more slowly than air?
Since glass has a higher density than air, light waves go through it more slowly than they do through it.
Can Light pass through vacuums?
Yes light can pass through vacuum
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...