The length of the line segment connecting two points is defined as the distance between them. The length of the line segment connecting the specified coordinates can be used to compute the distance between two points in coordinate geometry. Let’s look at the formula for calculating the distance between two points in a two-dimensional or three-dimensional plane.
What is the Distance Between Two Points?
The distance of the line segment connecting any two points is the distance between them. There is only one line that connects two points. As a result, the distance between two points may be computed by determining the length of the line segment that connects the two spots. For example, if A and B are two points and A B = 20 cm, it implies the distance between A and B is 20 cm.

The length of the line segment connecting two points is the distance between them (but this CANNOT be the length of the curve joining them). It is important to note that the distance between two places is always positive.
Distance Between Two Points Formula
The distance formula is used to determine the distance between two points using the provided coordinates. We use the 2D distance formula or the Euclidean distance formula to calculate the distance between any two points in the 2-D plane.
Formula for Distance Between Two Points
The formula for the distance, d, between two points whose coordinates are (x1, y1) and (x2, y2) is
![Rendered by QuickLaTeX.com d = \sqrt{[(x_2 - x_1 )^2 +(y_2 - y_1)^2]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3140d87c791fc103f4ae8e1bc9f1f6b6_l3.png)
This is called the Distance Formula.
To find the distance between two points given in 3-D plane, we can apply the 3D distance formula, given as,
![Rendered by QuickLaTeX.com d = \sqrt{[(x_2 - x_1 )^2 +(y_2 - y_1)^2 + (z_2 - z_1 )^2]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e775ca601d2ff593f3df5bccca855f9e_l3.png)
Derivation of Formula for Distance Between Two Points
To obtain the formula for calculating the distance between two points on a two-dimensional plane, assume there are two points with the coordinates, A (x1,y1) and B (x2,y2). Following that, we will suppose that the line segment connecting A and B is AB = d. We will now plot the specified points on the coordinate plane and connect them with a line.

Next, we will construct a right-angled triangle using AB as the hypotenuse.
Using Pythagoras Theorem,
AB2 = AC2 + BC2
d2 = (x2−x1)2 + (y2−y1)2
Here, the vertical distance between the given points is | y2 – y1|
The horizontal distance between the given points is | x2 – x1 |
![Rendered by QuickLaTeX.com d = \sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2] }](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-03fd85f85b23beb381f3f8e3c5e7106d_l3.png) (Taking square root on both sides)
(Taking square root on both sides)
Thus, the distance formula to find the distance between two points is proved.
Using similar steps and concept, we can also derive the formula to find the distance between two points given in the 3D plane.
Steps to find the distance between two points
The following steps may be used to determine the distance between two places using the provided coordinates:
- Make a note of the coordinates of the two given points on the coordinate plane as follows: A(x1,y1) and B(x2,y2).
- We may use the distance formula to calculate the distance between two places,
![Rendered by QuickLaTeX.com d = \sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2]}.](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-66d2cf4b660d0aea364034dcad27d1fb_l3.png)
- Express the given answer in units.
Note: We can apply the 3D distance formula in case the two points are given in 3D plane,
Sample Problems
Problem 1: Find the distance between the two points with the coordinates given as, A(1,5) and B (2,7).
Solution:
Let (x1, y1) be (2,7) and (x2, y2) be (1,5).
The distance d between the points : ![Rendered by QuickLaTeX.com d = \sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-eccfde3b56ba87fa0e65a686b3429096_l3.png)
![Rendered by QuickLaTeX.com \implies \sqrt{[(2-1)^2 + (7-5)^2]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b00912643603518992ad8abc535c9819_l3.png)
![Rendered by QuickLaTeX.com \implies \sqrt{[1^2 + 2^2]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7f53e212f303b34f9002e1df88a99b2c_l3.png)

The distance between the two points is √5 units.
Problem 2: Find the distance between the two points with the coordinates given as, P (2,-6,2) and Q(7, 3, 1).
Solution:
Let (x1, y1, z1) be P (2,-6,2) and (x2, y2, z2) be Q (7,3,1).
The distance d between the points P and Q : ![Rendered by QuickLaTeX.com d = \sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2+(z_2-z_1)^2]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d3fe5a616f5a474420d2f53853d99518_l3.png)
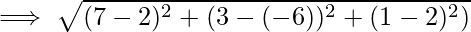
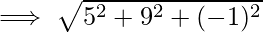
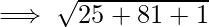
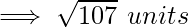
Problem 3: Prove that the vertices of a right-angled triangle are the points (3, 4), (7, 4), and (3, 8).
Solution:
Let us say the given points be:
P = (3, 4)
Q = (7, 4)
R = (3, 8)

Now, we will find each vertices of the right-angle triangle by distance formula.
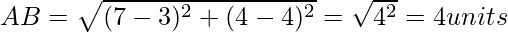
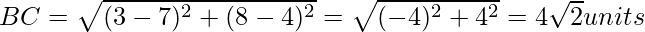
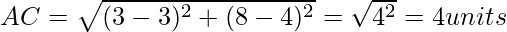
As we know the length of the sided of the right-angled triangle, by Pythagoras Theorem;
AB2 + AC2 = BC2
42+42=(4√2)2
16+16 = 32⟹32 = 32
This proves that ABC is a right-angle triangle.
Distance Between Two Points in Complex Plane
The distance between two points in a complex plane or two complex numbers z1=a+ib and z2=c+id in the complex ⟹1−2k=9+4k plane is the distance between points (a, b) and (c, d), given as,
![Rendered by QuickLaTeX.com | z_2 - z_1 |= \sqrt{[(a − c)^2 + (b − d)^2]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-759a065ac7716c62761c0b270e2ad16d_l3.png)
Problem 4: Find the distance between the two complex numbers z1 = 2−5i and z2 = 7+7i
Solution:
Here, we have two complex numbers z1 = 2-5i and z2 = 7+7i.
The distance between these complex numbers is equidistance to the two points in the plane, with coordinates, (2,-5) and (7,7).
Thus, distance between the two points is
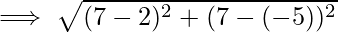
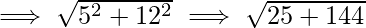

Hence, the distance between two complex numbers z_1=2-5i and z_2=7+7i is 13 units.
Problem 5: A complex number ω is 6 units apart from z1 = -3 – i and 6 units apart from z2 = 3 + 5i. Check whether the triangle formed by ω, z1, z2 is right – angled or not.
Solution:
There are 3 complex numbers ω, z1, z2.
As we know the distance between ω and z1 is 6 units and distance between ω and z2 is 6 units.
Given, ω, z1 = 6 units
ω, z2 = 6 units
Now, we will find the distance between z1 and z2 by using distance formula.
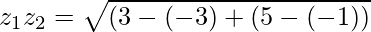
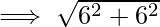

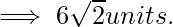
By Pythagoras Theorem, we have;
(z1z2)2=(ωz1)2+(ωz2)2
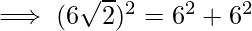

Hence, we conclude that the given triangle is right-angle triangle.
Problem 6: Find a point on the x-axis that is equidistant from the points (1, -2) and (-2, -3).
Solution:
We know that any point on the x-axis has an y-coordinate of 0. As a result, we consider the point equidistant from the provided points to be (k,0). i.e., Distance between ( k,0) and (1, -2) = Distance between (k, 0) and (-2, -3).
![Rendered by QuickLaTeX.com \implies \sqrt{[(1-k)^2 + (-2-0)^2]} = \sqrt{[(-2-k)^2 + (-3-0)^2]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c25e8ce966bde683d918dee4c5553bd8_l3.png)
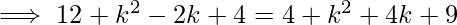
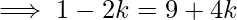
\implies -4k-2k= 9-1
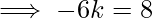

Therefore, the required point is (k, 0) = 
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...