How to calculate the average of a set of numbers?

Question

GeeksforGeeks · Accepted Answer

The mean or average of the given data distribution is the calculated central value. It is used to determine the average of the given data. It gives a measure of the central tendency of the data. The central tendency of data distribution is the statistical measure that represents and identifies the entire data distribution using a single value. It acts as an exact descriptor of the data represented.

In statistics, the mean of the data can also be defined as the sum of all observations to the total number of observations. The mean of data distribution is also known as the arithmetic mean or average. It is denoted by x̄.

⇒ Given a data set with total n values,

X = x₁, x₂,…, x_n, the mean x̄ is the mean of the n values x₁, x₂,…, x_n.

Mean Formula

$Mean\ =\ \frac{Sum\ of\ observations}{Number\ of\ observations}$

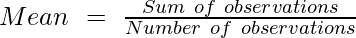
Mean Formula For Ungrouped Data

The formula to compute the mean in case of ungrouped data:

Let us assume, x₁, x₂, x₃,……, x_n be n observations of a data set.

Then we have,

The mean of these values is:

$x̄ = \frac{∑x_i}{n}$

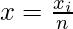
Here, we have,

x_i = ith observation, 1 ≤ i ≤ n

∑x_i = Sum of observations

n = Number of observations

Mean Formula For Grouped Data

The mean of the data is dependent on the computation of mean in the case of grouped data :

Direct Method
Assumed Mean Method
Step-deviation Method

Calculating Mean Using Direct Method

The direct method is one of the easiest and simplest methods used to compute the mean of the grouped data. The following steps can be used to compute the mean of the given data distribution:

Step 1: Create a table having four columns as computed below,

Column 1- Class interval.
Column 2- Class marks, denoted by xi.
Column 3- Corresponding Frequencies (f_i)
Column 4- x_if_i,which is the product of column 2 and column 3.

Step 2: Computing Mean by the Formula Mean, we have = 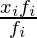$\frac{∑x_if_i}{∑f_i}$

Calculating Mean Using Assumed Mean Method

The direct method used for the computation of the mean is a tedious method. The assumed mean method can be used in order to compute the mean of a set of grouped data. The following steps can be used to compute the mean of the given data distribution:

Step 1: Create a table having five columns as computed below,

Column 1- Class interval.
Column 2- Classmarks, denoted by xi. The central value of this column is taken as the Assumed Mean. This is denoted by A.
Column 3- Corresponding deviations are then computed. The column values are computed as follows, i.e. d_i = x_i – A
Column 4- Corresponding Frequencies (f_i)
Column 5- Mean of d_ivalues of Column 3 is computed using formula. Therefore, mean of d_i = 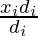$\frac{∑x_id_i}{∑d_i}$

Step 2: At last, compute the mean of the given data distribution by performing the summation of the data to find the assumed mean to the mean of the d_i.

Calculating Mean Using Step Deviation Method

Also known as the shift of origin and scale method, the step deviation method is used to eliminate performing tedious calculations for computation of grouped data mean. The following steps can be used to compute the mean of the given data distribution:

Step 1: Create a table containing five columns as given below,

Column 1- Class interval.
Column 2- Classmarks, denoted by x_i. The central value of this column is taken as the Assumed Mean. This is denoted by A.
Column 3- Corresponding deviations are then computed. The column values are computed as follows, d_i = x_i– A
Column 4- Calculate the values of u_i using the formula, u_i= 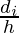$\frac{d_i}{h}$ , where h is the class width.
Column 5- Corresponding Frequencies (f_i)

Step 2: Therefore, the Mean of u_i = 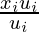$\frac{∑x_iu_i}{ ∑u_i}$

Step 3: At last, compute the mean of the given data distribution by calculating the Mean by performing the summation of the assumed mean A to the product of class width(h) with mean of u_i.

Sample Questions

Question 1. Calculate the mean of the following data.

5, 10, 4, 20, 25, 18, 11, 13, 19, 22

Solution:

Here we have been given,

x_i = 5, 10, 4, 20, 25, 18, 11, 13, 19, 22

n = 10

Mean x̄ = 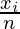$\frac{∑x_i}{n}$

= $\frac{5+ 10+ 4+ 20+ 25+ 18+ 11+ 13+ 19+ 22}{10}$

= $\frac{147}{10}$

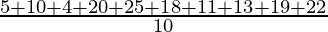
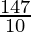
= 14.7

Hence,

The mean of this data is 14.7.

Question 2. Calculate the mean of the data for the distribution below of marks obtained by students in exams?

Marks	50	86	76	84	66	56	58	40
Number of students	40	2	8	4	30	48	56	12

Solution:

Finding the sum:

Marks (x_i) Number of students (f_i) f_ix_i
50 40 1000
86 2 86
76 8 304
84 4 168
66 30 990
56 48 1344
58 56 1624
40 12 240
Sum 200 5756

Mean = 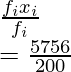$\frac{∑f_ix_i}{∑f_i}\\ =\frac{5756}{200}$

= 28.78

Therefore,

The mean of the following distribution is 28.78.

Question 3. Assume if in a class the height of 5 girls is 140 cm, 152 cm, 150 cm, 153 cm, and 154 cm. Then find the mean of the height of the girls?

Solution:

Here we are given height of girls

140 cm, 152 cm, 150 cm, 153 cm, and 154 cm

$Mean\ =\ \frac{Sum\ of\ observation}{Number\ of\ observation}$

$=\frac{140+ 152+ 150 + 153 + 154 }{5}\\ =\frac{749}{5}$

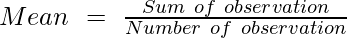
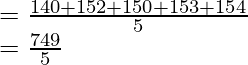
= 149.8

Therefore,

Mean, x̄ =149.8 cm.

Question 4. Find the mean of the first five natural numbers?

Solution:

First five natural are 1, 2, 3, 4 and 5

Further,

Mean of the first five natural numbers = 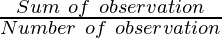$\ \frac{Sum\ of\ observation}{Number\ of\ observation}$

$=\frac{1+2+3+4+5}{5}\\ =\frac{15}{5}$

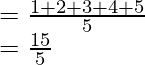
= 3

Thus,

The mean of first five natural numbers is 3.

Question 5. Find the mean of the first 10 prime numbers?

Solution:

The first 10 prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.

Further,

Mean of the first five natural numbers = 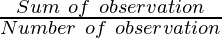$\ \frac{Sum\ of\ observation}{Number\ of\ observation}$

$=\frac{ 2+ 3+ 5+ 7+ 11+ 13+ 17+ 19+ 23+29 }{10}\\ =\frac{129}{10}$

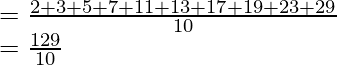
= 12.9

Thus,

The mean of first 10 prime numbers is 12.9.