How to calculate probability in a normal distribution given mean and standard deviation in Python?
Last Updated :
25 Feb, 2021
A normal distribution is a type of continuous probability distribution for a real-valued random variable. It is based on mean and standard deviation. The probability distribution function or PDF computes the likelihood of a single point in the distribution. The general formula to calculate PDF for the normal distribution is
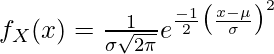
Here,
- µ is the mean
- σ is the standard deviation of the distribution
- x is the number
for which PDF is to be calculated.. We can calculate probability in a normal distribution using SciPy module.
Installation:
pip install scipy
Function used:
We will use scipy.stats.norm.pdf() method to calculate the probability distribution for a number x.
Syntax: scipy.stats.norm.pdf(x, loc=None, scale=None)
Parameter:
- x : array-like object, for which probability is to be calculated.
- loc : optional (default=0), represents mean of the distribution.
- scale : optional (default=1), represents standard deviation of the distribution.
Returns: A probability density function calculated at x as a ndarray object.
In scipy the functions used to calculate mean and standard deviation are mean() and std() respectively.
Syntax:
mean(data)
Syntax:
std(data)
Approach
- Import module
- Create necessary data
- Supply the function with required values
- Display value
Example:
Python3
from scipy.stats import norm
import numpy as np
data_start = -5
data_end = 5
data_points = 11
data = np.linspace(data_start, data_end, data_points)
mean = np.mean(data)
std = np.std(data)
probability_pdf = norm.pdf(3, loc=mean, scale=std)
print(probability_pdf)
|
Output:
0.0804410163156249
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...