How to calculate P Value?
Last Updated :
10 May, 2020
P-value, also referred to as probability value is a statistical measure used to determine whether to accept or reject the Null Hypothesis, considering the Null Hypothesis to be True.
For calculating the p-value, we perform an experiment and based on the observations of the test-statistic we make decisions, i.e., if the measure is statistically below the significance level, the Null Hypothesis is rejected, specifying that the Null Hypothesis is very less likely to occur.
How it works?
Consider, there is a magazine that says, on an average there are 12% Indian employees in a company in US.
Assumptions:
- Test-statistic: An average company has 12% Indian employees, i.e., μ (Population) = 0.12.
- Null Hypothesis (H0) : There are 12% of Indian employees in a company.
- Alternative Hypothesis (Ha) : There are more than 12% of Indian employees in a company in US.
- Significance Level: α = 0.05 (generally a low value)
- Sample statistic: We take a company X and we check for 50 employees and find that more than 20% are Indian.
We perform n experiments, and if probability of getting the sample statistic, given there are 12% Indian employees, for n observations (p-value) is less than 0.05 we Reject the Null Hypothesis and Accept the Alternative Hypothesis, otherwise we do not Reject the Null Hypothesis.
p-value = P( μ (sample) > 20% | H0 is True )
Methods to determine P Value
By Simulation
We simulate the situation and take samples that provide our Null Hypothesis to be True. In the above example, we take 20 samples of 50 employees each, and in each sample, there are 12% of Indian employees (Null Hypothesis). We re-sample 20 samples of 50 employees each from the above-collected samples.
Below are the results of the simulation:
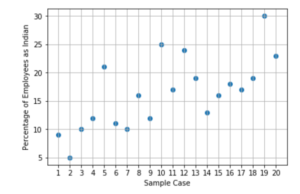
There are 5 samples out of 20 which had more than 20% employees as Indian.
Hence, the p-value would be 5/20 = 0.25.
Since the significance level was 5% and after simulation, the value obtained 25%, we cannot reject the Null Hypothesis.
z Statistic
To perform z-test, three conditions are required to be met for the samples we collect:
- Random: The sampling of data to be purely random.
- Normal: The data needs to be roughly normally distributed.
- Independent: The sample must be independent from the previous sample, i.e., we need to perform the sampling with replacement, or, we can check if the sample is less than 10% of its population.
Assuming the three conditions are met, z value is calculated by looking at the standard deviation between the sample statistic and the population proportion.
For z test, the mean is not considered, instead, we take the proportions to calculate p value.
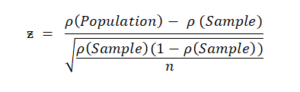
Here, ρ(Population)=12%, ρ(Sample)=20% and n=50 (Considering the ρ, i.e., proportion to be same as mean)
We get, z = -0.004
The p value is obtained from z table for above z value, which is 0.4840, i.e., roughly 48%.
Since the significance level was 5% and we obtained 48%, we cannot reject the Null Hypothesis.
t Statistic
In t test, all the three conditions are as required by z-test, i.e., the sample should be random, normal, and independent.
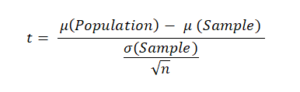
Here, μ(Population)=12%, μ(Sample)=20%, σ(Sample), i.e., the standard deviation of sample to be 5, and n=50.
Then, t = -0.113
For t-Test we look into the t table to find the p-value, the degree of freedom (df) is n-1, i.e., 49 and we look for a value in row 49 to be equal or greater than t, and obtain the corresponding y value to get p-value to be roughly 45%.
Since the p-value is 45% and we have a significance level to be 5%, we cannot reject the Null Hypothesis.
Note: When considering means, t-test is used, and when considering proportions, z test is used.
Share your thoughts in the comments
Please Login to comment...