How many faces, edges, and vertices does a cube have?
Last Updated :
18 Feb, 2024
Cube is a 3-Dimensional Figure in which all dimensions are equal. A cube has 6 Square faces as all the sides of a cube are equal. The boundary where the faces of the cube meet are called the cube edges. The point at which the cube edges meet is called the cube vertices. A cube has 12 Edges and 8 vertices. In this article, we will learn about cube edges faces vertices in detail with a brief introduction to cubes.
What is a Cube?
A Cube is a 3-Dimensional Solid figure whose all faces are square shaped. We can also say that a cube can be visualized in the form of a square prism. This is because the faces of a cube are in the form of a square and are also platonic solid in nature. The faces of a cube are also known as planes.
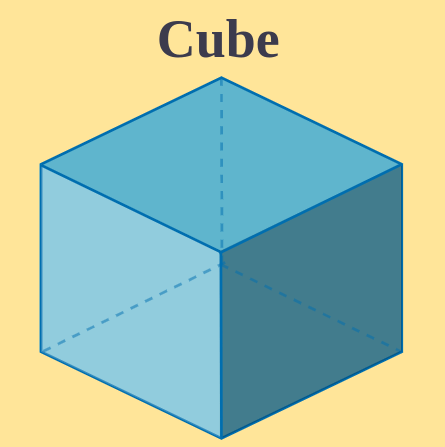
Properties of a Cube
The properties of a cube are mentioned below:
- All the faces are square-shaped, which implies that the length, breadth, and height are the same.
- The angles between any two faces or surfaces are equivalent to 90°.
- The opposite planes are parallel to each other.
- The opposite edges are parallel to each other.
- Each of the faces forms an intersection with four faces.
- Each of the vertices intersects with three faces and three edges.
Cube Examples
Examples of Cube include, Rubik’s Cube, Ice Cube, Die used in Ludo, Cubical Box Etc. A picture of examples of a Cube is attached below:

How many Faces, Edges, and Vertices does a Cube have?
There are 6 faces, 12 edges, and 8 vertices in a cube. Let’s look into them in detail:
Faces in Cube
There are six faces in a cube. The faces in a cube are in the shape of a square. Faces are flat surfaces bounded by line segments on four sides called edges. We can realize there are six faces in a cube by seeing the number written 1 to 6 on the faces of the die of Ludo.
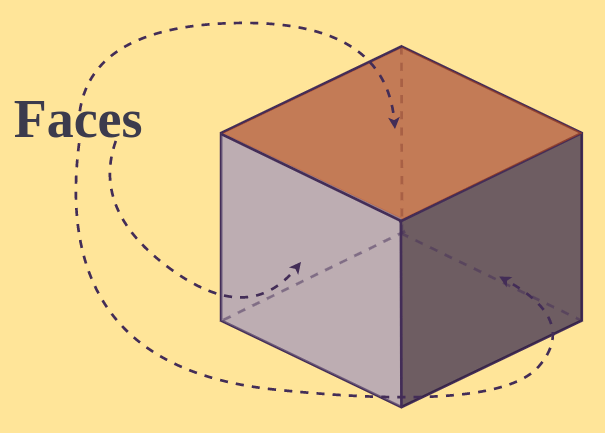
Edges in cube
There are 12 Edges in a Cube. Edges are the boundary of a flat surface. Edges are the line segment where are two faces of a geometrical figure. Edges meet each other at a point called Vertices.
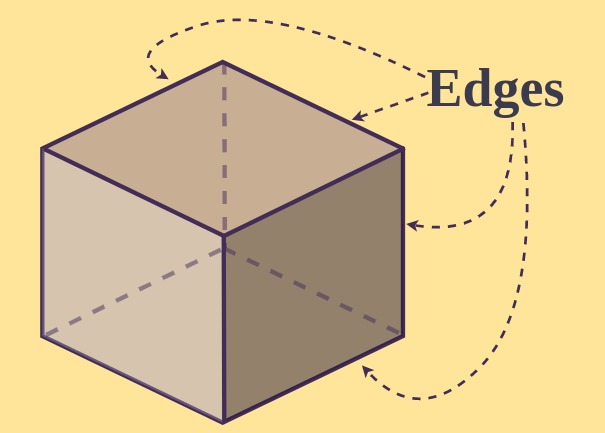
Vertices in Cube
There are 8 vertices in a Cube. Vertices are the points where edges meet. In a cube, a minimum of three edges meet at a vertex. Vertices are the corners of the cube. Vertices are dimensionless.
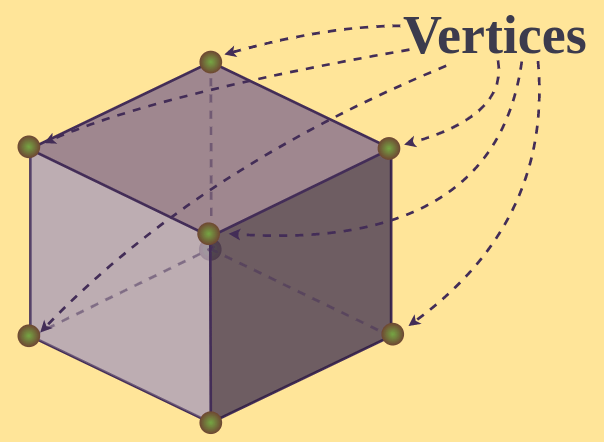
Learn more about Vertices, Edges, and Faces.
Formula of Cube
A cube is a 3D figure. Hence, it will occupy space which is called the volume of the cube. Each face has an area that combines to give up the surface area of the cube. Let’s learn the Formula of the Cube. Let us assume each side of the cube measures ‘a’ units. Hence formulas for this cube are given as:
- Volume of Cube = (Side)3 = a3 cubic units
- Total Surface Area of the Cube = 6 ⨯ (side)2 = 6a2 square units
- Lateral Surface Area of the Cube = 4 ⨯ (side)2 = 4a2 square units
- Diagonal of Cube = √3 ⨯ side = √3 a units
Read More
Sample Problems on Cube Faces Edges and Vertices
Problem 1: Find the surface area of the cube if its side is 6 cm
Solution:
Given:
Side of the cube = 6 cm
As we know that
Surface area of the cube = 6 × side × side
⇒ Surface area of the cube = 6 × side2
⇒ Surface area of the cube = 6 × 62
⇒ Surface area of the cube = 216 cm2
Therefore,
Surface area of the cube is 216 cm2.
Problem 2: Find the volume of the cube if its side is 4 m2.
Solution:
Here we need to find the volume of the cube
Given:
Side of the cube = 4 m2
As we know that
Volume of the cube = Side × Side × Side
⇒ Volume of the cube = Side3
⇒ Volume of the cube = 43
⇒ Volume of the cube = 4 × 4 × 4
⇒ Volume of the cube = 64 m3
Therefore,
Volume of the cube is 64 m3.
Problem 3: Find how many small cubes can be made from a big cube of side 16 m in small cubes of side 4 m
Solution:
Here we need to find out how many small cubes can be made out of one big cube.
As we know that
Volume of cube = Side3
⇒ Volume of big cube = Side × Side × Side
⇒ Volume of big cube = 16 × 16 × 16
⇒ Volume of big cube = 163
⇒ Volume of big cube = 4096 m3
Further,
Volume of small cube = Side × Side × Side
⇒ Volume of small cube = 4 × 4 × 4
⇒ Volume of small cube = 43
⇒ Volume of small cube = 64 m3
Now,
Number of small cubes that can be made from the big cubes = Volume of big cube/Volume of small cube
⇒ Number of small cubes = 4096/64
⇒ Number of small cubes = 64
Therefore,
64 small cubes will be made out of the big cube.
Problem 4. If the surface area of a cube is 486 m2. Then find the volume of the cube.
Solution:
Here we need to find the volume of the cube from a given surface area
Given that Surface area of the cube = 486 m2
As we know that
Surface area of the cube = 6 × Side2
⇒ 486 = 6 × Side2
⇒ Side2 = 486/6
⇒ Side2 = 81
⇒ Side = √81
⇒ Side = 9 m
Now,
Volume of cube = Side3
⇒ Volume of cube = 93
⇒ Volume of cube = 9 × 9 × 9
⇒ Volume of cube = 729 m3
Therefore,
Volume of the cube is 729 m3.
FAQs on Cube Faces Edges and Vertices
Q1: Define Cube.
Answer:
A Cube is a three-dimensional figure whose each face is a square.
Q2: How many Faces are there in a Cube?
Answer:
In a cube there are six faces.
Q3: How many Edges are there in a Cube?
Answer:
There are 12 Edges in a Cube.
Q4: How many Vertices are there in a Cube?
Answer:
A cube has 8 vertices.
Q5: What are the Cube Formulas?
Answer:
The formula for cube is given below:
- Volume of cube = (side)3
- Total Surface Area of Cube = 6 ⨯ (side)2
- Lateral Surface Area of Cube = 4 ⨯ (side)2
- Diagonal of Cube = √3 ⨯ side
Share your thoughts in the comments
Please Login to comment...