How many different combinations of nickels, dimes and quarters can a piggy bank contain if it has 20 coins in it?

Given a definite number of elements, their different arrangements, either by choosing one after the other, or some of them, or all of them at a time are called permutations. They are regarded as the process of assigning a linear sequence to the members of a given sequence. It is also referred to as the process of re-ordering the elements of a given sequence or series. In other words, to permutate a sequence means to list out all possible arrangements of that sequence For example, the series {1, 2} can be written in two ways: either as {1, 2} or {2, 1}.

Permutation Formula

Number of permutations when r number of elements are arranged out of n elements in a given sequence 

ⁿP_r = n! / (n – r)!

For example, let n = 5 and r = 2. The number of permutations is ⁵P₂ = 5! / (5 – 2)! = 20. 

Combinations

It is defined as the process of selecting either one or two or some elements from a given sequence, regardless of the order of the elements. Say, two elements of a series are to choose which only has 2 elements, to begin with, then the order of those elements won’t matter.

Combination Formula 

Number of combinations when r number of elements are selected out of n elements in a given sequence 

ⁿC_r = n! / r! (n – r)!

For example, let n = 5 and r = 2, then number of ways to select 2 elements out of 5 = ⁵C₂ = 5! / 2! (5 – 2)! = 10.

A point worth noting is that in case r number of combinations are to be derived from a set with n elements, where repetition of such elements is allowed, then,

^n+r−1C_r = ^n+r−1C_n−1.

Find the number of combinations a piggy bank contains, of nickels, dimes, and quarters given that it has 20 coins in it.

Solution:

Clearly order of the coins does not matter in this question. Also there is no mention as to whether repetition is allowed or not. 

Following the rule, there are in case of r number of combinations from a sequence having n number of elements where elements can be repeated ^n+r−1C_r = ^n+r−1C_n−1, we have:

Number of combinations = ^20+3-1C₂₀ = ²²C₂₀

= 22! / (22 – 20)! 20! 

= 11 × 21

= 231

Similar Problems

Question 1. Tell the number of ways for assigning 7 students on a college trip given that we have 1 triple and 2 double rooms.

Solution:

This problem can be interpreted as having to put the 7 students into groups of 3, 2 and 2.

Number of ways to choose 3 students in the triple = ⁷C₃ = 7! / 3!4! = 35  

Number of ways to choose 2 out of the remaining 4 students = ⁴C₂ = 4!/ 2!2! = 6

Number of ways to choose 2 students out of the remaining two students = 1

Total number of arrangements = 35 × 6 × 1 = 210.

Hence, 7 students can be assigned to 1 triple and 2 double hotel rooms during a conference in 210 ways.

Question 2. Find the number of ways in which a committee of five persons can be formed if they are to be selected from a group of 7 men and 6 women, so as to have at least 3 men on there.

Solution:

At least three men on the committee means we can have either exactly three, four or all five men in the committee.

Number of arrangements when there are 3 men and 2 women on the committee = (⁷C₃ x ⁶C₂) = 525

Number of arrangements when there are 4 men and 1 woman on the committee=  (⁷C₄ x ⁶C₁) = 210

Number of arrangements when there are all 5 men on the committee = (⁷C₅) = 21

Total arrangements = 525 + 210 + 21

= 756

Question 3. Find the number of arrangements of the letters of the word ‘LEADING’ where the vowels always appear together?

Solution:

If the vowels are to appear together, they would form a separate letter in the word. Hence we are left with 4 + 1 = 5 letters, which can be arranged in 5! = 120 ways.

Furthermore, there are 3! = 6 ways to arrange the vowels together.

Total number of ways of arranging the letters = 120 x 6 = 720.

Question 4. Find the number of words having 4 consonants and 3 vowels which can be formed out of 8 consonants and 5 vowels.

Solution:

Number of ways of selecting 4 consonants out of 8 and 3 vowels out of 5 = ⁸C₄ x ⁵C₃

= 

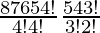
= 70 × 10 = 700

Number of ways of arranging the 7 letters among themselves = 7! = 5040

Number of words that can be formed = 5040 × 700 = 3528000.

Question 5. How many four-letter words can be made out of the word ‘GEEKSFORGEEKS’ if repetition is not allowed?

Solution:

Since there are 7 different letters in the word ‘GEEKSFORGEEKS’

Required number of words = ⁷P₄

= 7! / 3!

= 840