How many committees can be made from 15 people that have at least 2 people in each committee?
Last Updated :
20 Nov, 2021
In mathematics, permutation is known as the process of arranging a set in which all the members of a set are arranged into some series or order. The process of permuting is known as the rearranging of its components if the set is already arranged. Permutations take place, in more or less important ways, in almost every area of mathematics. They frequently appear when different commands on certain finite sets are considered.
Combination
A combination is an act of choosing items from a group, such that (not like permutation) the order of choice does not matter. In smaller cases, it is possible to count the number of combinations. Combination refers to the union of n things taken k at a time without repetition In combination you can select the items in any order. To those combinations in which re-occurrence is allowed, the terms k-selection or k-combination with replication are frequently used.
Permutation Formula
In permutation r things are selected from a set of n things without any replacement. In this order of selection matter.
nPr = (n!) / (n – r)!
n = set size, the total number of items in the set
r = subset size, the number of items to be selected from the set
Combination Formula
In combination r things are selected from a set of n things and where the order of selection does not matter.
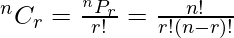
Here, n = Number of items in set
r = Number of items selected from the set
How many committees can be made from 15 people that have at least 2 people in each committee
Solution:
Since order doesn’t matter
Use the combination formula, n! ⁄ r!(n – r)!
Explanation:
n = 15, the total number of people
r = 2, the number of people being picked
Enter n and r into the formula:
= 15! ⁄ 2!(15 – 2)!
= 15! ⁄ 2!(13)!
= 150
So, there are 150 different committees that can be formed.
Similar Problems
Question 1: How many different 2 people committees can be formed from a group of 24 people?
Solution:
Since order doesn’t matter,
Use the combination formula, nCr = n! ⁄ r!(n – r)!
Explanation:
n = 24, the total number of people,
r = 2, the number of people being picked
Enter n and r into the formula:
= 24! ⁄ 2!(24 – 2)!
= 24! ⁄ 2!(22)!
= 276
So, there are 276 different committees that can be formed.
Question 2: How many different 4 people committees can be formed from a group of 25 people?
Solution:
Since order does not matter,
Use the combination formula, nCr = n! ⁄ r!(n – r)!
Explanation:
n = 25, the total number of people,
r = 4, the number of people being picked
Enter n and r into the formula:
= 25! ⁄ 4!(25 – 4)!
= 25! ⁄ 4!(21)!
= 12650
So, there are 12650 different committees that can be formed.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...