How many bit strings of length 9 have exactly 4 0’s?
Last Updated :
30 Nov, 2021
Permutations and combinations are a branch of mathematics that deals with the study of the selection of a subset of items from the entire collection. In combinations, the order of selection of items doesn’t matter. The items can be rearranged into the desired format. For instance, there are three alphabets A, B, and C. If we have to select two alphabets from it, then we have, AB, BC, and AC. Here, the selection of AB is equivalent to the selection of BA.
However, in case the numbers are too large, these calculations can’t be done manually. Therefore, we have,
nCr = 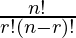
where n = total items to pick
r = the items to choose
Therefore, in the state example,
nCr = 3C2
= 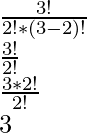
How many bit strings of length 9 have exactly 4 0’s?
Solution:
We have,
Total number of places to choose from = 9
The number of places to fill with 0’s = 4
Therefore, we have to fill 4 places with 0’s out of a total of 9 places.
According to the formula of combinations, where order of selection doesn’t matter.
nCr = 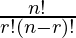
where n = total items to pick
r = the items to choose
Upon substituting the values we get,
=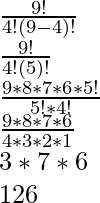
Therefore,
There are 126 ways to have 9-bit strings containing exactly 4 0’s.
Similar Questions
Question 1. Find out in how many ways a project team of 7 men and 10 women, may be chosen from the office of 9 men and 12 women?
Solution:
Here we have to find that in how many ways a project team can be selected in an office.
Thus,
To choose 7 men from 9 men
⇒ 9C5 ways = 9!/(9-5)!5!
⇒ 9!/4!5!
⇒ 9 × 8 × 7 × 6 × 5!/4 × 3 × 2 × 1 × 5!
⇒ 3024/24
= 126
Further,
To choose 10 women from 12 women
⇒ 12C10 = 12!/(12 – 10)!10!
⇒ 12 × 11 × 10!/2!10!
⇒ 132/2
⇒ 66
Therefore
The project team can be chosen in the
⇒ 66 × 126 ways
⇒ 8316 ways
Question 2. Find out C(25, 23). C(n, r) = n!/(n – r)!r!
Solution:
Here we have,
n = 25
r = 23
Substituting the values of n and r in C(n, r) = n!/(n – r)!r!
⇒ C(25, 23) = 25!/(25 – 23)!23!
⇒ C(25, 23) = 25!/(2)!23!
⇒ C(25, 23) = 25 × 24 × 23!/2! × 23!
⇒ C(25, 23) = 25 × 24/ 2
⇒ C(25, 23) = 600/2
⇒ C(25, 23) = 300
Therefore,
⇒ C(25, 23). C(n,r)=n!/(n – r)!r! = 300
Question 3. Find out in how many ways lights in a chandelier having 6 small lights and 8 big lights, can be selected from 8 small lights and 10 big lights?
Solution:
Here we have to select lights for the chandelier
First finding the selection for small lights
Selecting, 6 small lights from 8 small lights
⇒ 8C6 = 8!/(8-6)!6!
⇒ 8!/2!6!
⇒ 8 × 7 × 6!/2 × 1 × 6!
Solving
⇒ 56/2
⇒ 28
⇒ 8C6 = 28
Therefore,
Small lights can be selected in 28 ways
Further selecting big lights
Selecting, 8 big lights from 10 big light
⇒ 10C8 = 10!/(10 – 8)!8!
⇒ 10!/2!8!
⇒ 10 × 9 × 8!/2 × 1 × 8!
Solving
⇒ 90/2
⇒ 45
10C8 = 45
Thus,
Big lights can be selected in 45 ways
Therefore,
Small and big lights in a chandelier can be selected in
⇒ 28 × 45
⇒ 1260 ways
Question 4. Find out C(15, 13). C(n, r) = n!/(n – r)!r!
Solution:
Here we have,
n = 15
r = 13
Substituting the values of n and r in C(n, r) = n!/(n – r)!r!
⇒ C(15, 13) = 15!/(15 – 13)!13!
⇒ C(15, 13) = 15!/(2)!13!
⇒ C(15, 13) = 15 × 14 × 13!/2! × 13!
⇒ C(15, 13) = 15 × 14/2
⇒ C(15, 13) = 210/2
⇒ C(15, 13) = 105
Therefore,
⇒ C(15, 13). C(n,r)=n!/(n – r)!r! = 105
Question 5. Find out C(50, 47). C(n, r) = n!/(n – r)!r!
Solution:
Here we have,
n = 50
r = 47
Substituting the values of n and r in C(n, r) = n!/(n – r)!r!
⇒ C(50, 47) = 50!/(50 – 47)!47!
⇒ C(50, 47) = 50!/(3)!47!
⇒ C(50, 47) = 50 × 49 × 48 × 47!/3! × 47!
⇒ C(50, 47) = 50 × 49 × 48/3 × 2
⇒ C(50, 47) = 117600/6
⇒ C(50, 47) = 19600
Therefore,
⇒ C(50, 47). C(n,r)=n!/(n – r)!r! = 19600
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...