How many bit strings of length 9 have exactly 4 0’s?

Permutations and combinations are a branch of mathematics that deals with the study of the selection of a subset of items from the entire collection. In combinations, the order of selection of items doesn’t matter. The items can be rearranged into the desired format. For instance, there are three alphabets A, B, and C. If we have to select two alphabets from it, then we have, AB, BC, and AC. Here, the selection of AB is equivalent to the selection of BA.

However, in case the numbers are too large, these calculations can’t be done manually. Therefore, we have, 

ⁿC_r =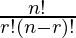

where n = total items to pick

r = the items to choose

Therefore, in the state example, 

ⁿC_r = ³C₂

= 

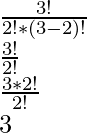
How many bit strings of length 9 have exactly 4 0’s?

Solution: 

We have,

Total number of places to choose from = 9 

The number of places to fill with 0’s = 4

Therefore, we have to fill 4 places with 0’s out of a total of 9 places.

According to the formula of combinations, where order of selection doesn’t matter. 

ⁿC_r =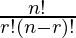 

where n = total items to pick

r = the items to choose

Upon substituting the values we get,

=

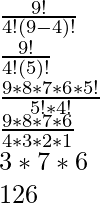
Therefore, 

There are 126 ways to have 9-bit strings containing exactly 4 0’s. 

Similar Questions

Question 1. Find out in how many ways a project team of 7 men and 10 women, may be chosen from the office of 9 men and 12 women?

Solution:

Here we have to find that in how many ways a project team can be selected in an office.

Thus,

To choose 7 men from 9 men

⇒ ⁹C₅ ways = 9!/(9-5)!5!

⇒ 9!/4!5!

⇒ 9 × 8 × 7 × 6 × 5!/4 × 3 × 2 × 1 × 5!

⇒ 3024/24

= 126

Further,

To choose 10 women from 12 women

⇒ ¹²C₁₀ = 12!/(12 – 10)!10!

⇒ 12 × 11 × 10!/2!10!

⇒ 132/2

⇒ 66

Therefore

The project team can be chosen in the

⇒ 66 × 126 ways

⇒ 8316 ways

Question 2. Find out C(25, 23). C(n, r) = n!/(n – r)!r!

Solution:

Here we have,

n = 25

r = 23

Substituting the values of n and r in C(n, r) = n!/(n – r)!r!

⇒ C(25, 23) = 25!/(25 – 23)!23!

⇒ C(25, 23) = 25!/(2)!23!

⇒ C(25, 23) = 25 × 24 × 23!/2! × 23!

⇒ C(25, 23) = 25 × 24/ 2

⇒ C(25, 23) = 600/2

⇒ C(25, 23) = 300

Therefore,

⇒ C(25, 23). C(n,r)=n!/(n – r)!r! = 300

Question 3. Find out in how many ways lights in a chandelier having 6 small lights and 8 big lights, can be selected from 8 small lights and 10 big lights?

Solution:

Here we have to select lights for the chandelier

First finding the selection for small lights

Selecting, 6 small lights from 8 small lights

⇒ ⁸C₆ = 8!/(8-6)!6!

⇒ 8!/2!6!

⇒ 8 × 7 × 6!/2 × 1 × 6!

Solving

⇒ 56/2

⇒ 28

⇒ ⁸C₆ = 28

Therefore,

Small lights can be selected in 28 ways

Further selecting big lights

Selecting, 8 big lights from 10 big light

⇒ ¹⁰C₈ = 10!/(10 – 8)!8!

⇒ 10!/2!8!

⇒ 10 × 9 × 8!/2 × 1 × 8!

Solving

⇒ 90/2

⇒ 45

¹⁰C₈ = 45

Thus,

Big lights can be selected in 45 ways

Therefore,

Small and big lights in a chandelier can be selected in

⇒ 28 × 45

⇒ 1260 ways

Question 4. Find out C(15, 13). C(n, r) = n!/(n – r)!r!

Solution:

Here we have,

n = 15

r = 13

Substituting the values of n and r in C(n, r) = n!/(n – r)!r!

⇒ C(15, 13) = 15!/(15 – 13)!13!

⇒ C(15, 13) = 15!/(2)!13!

⇒ C(15, 13) = 15 × 14 × 13!/2! × 13!

⇒ C(15, 13) = 15 × 14/2

⇒ C(15, 13) = 210/2

⇒ C(15, 13) = 105

Therefore,

⇒ C(15, 13). C(n,r)=n!/(n – r)!r! = 105

Question 5. Find out C(50, 47). C(n, r) = n!/(n – r)!r!

Solution:

Here we have,

n = 50

r = 47

Substituting the values of n and r in C(n, r) = n!/(n – r)!r!

⇒ C(50, 47) = 50!/(50 – 47)!47!

⇒ C(50, 47) = 50!/(3)!47!

⇒ C(50, 47) = 50 × 49 × 48 × 47!/3! × 47!

⇒ C(50, 47) = 50 × 49 × 48/3 × 2

⇒ C(50, 47) = 117600/6

⇒ C(50, 47) = 19600

Therefore,

⇒ C(50, 47). C(n,r)=n!/(n – r)!r! = 19600

My Personal Notes arrow_drop_up

Save