Hopfield Neural Network
Last Updated :
13 Mar, 2024
The Hopfield Neural Networks, invented by Dr John J. Hopfield consists of one layer of ‘n’ fully connected recurrent neurons. It is generally used in performing auto-association and optimization tasks. It is calculated using a converging interactive process and it generates a different response than our normal neural nets.
Discrete Hopfield Network
It is a fully interconnected neural network where each unit is connected to every other unit. It behaves in a discrete manner, i.e. it gives finite distinct output, generally of two types:
- Binary (0/1)
- Bipolar (-1/1)
The weights associated with this network are symmetric in nature and have the following properties.
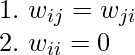
Structure & Architecture of Hopfield Network
- Each neuron has an inverting and a non-inverting output.
- Being fully connected, the output of each neuron is an input to all other neurons but not the self.
The below figure shows a sample representation of a Discrete Hopfield Neural Network architecture having the following elements.

Discrete Hopfield Network Architecture
[ x1 , x2 , ... , xn ] -> Input to the n given neurons.
[ y1 , y2 , ... , yn ] -> Output obtained from the n given neurons
Wij -> weight associated with the connection between the ith and the jth neuron.
Training Algorithm
For storing a set of input patterns S(p) [p = 1 to P], where S(p) = S1(p) … Si(p) … Sn(p), the weight matrix is given by:
![Rendered by QuickLaTeX.com w_{ij} = \sum_{p = 1}^{P} [2s_{i}(p) - 1][2s_{j}(p) - 1]\ (w_{ij}\ for\ all\ i\neq j)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c767d3ed8686a606560b3502e415ca93_l3.png)
![Rendered by QuickLaTeX.com w_{ij} = \sum_{p = 1}^{P} [s_{i}(p)s_{j}(p)]\ (where\ w_{ij} = 0\ for\ all\ i= j)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b99f66620dc94f93ad262aa6a429a51b_l3.png)
(i.e. weights here have no self-connection)
Steps Involved in the training of a Hopfield Network are as mapped below:
- Initialize weights (wij) to store patterns (using training algorithm).
- For each input vector yi, perform steps 3-7.
- Make the initial activators of the network equal to the external input vector x.
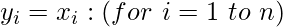
- For each vector yi, perform steps 5-7.
- Calculate the total input of the network yin using the equation given below.
![Rendered by QuickLaTeX.com y_{in_{i}} = x_i + \sum_{j} [y_jw_{ji}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c44fc8b7bb4b4393c59ec3fc7ed68ad2_l3.png)
- Apply activation over the total input to calculate the output as per the equation given below:
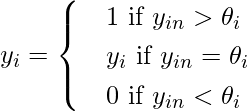
(where θi (threshold) and is normally taken as 0)
- Now feedback the obtained output yi to all other units. Thus, the activation vectors are updated.
- Test the network for convergence.
Consider the following problem. We are required to create a Discrete Hopfield Network with the bipolar representation of the input vector as [1 1 1 -1] or [1 1 1 0] (in case of binary representation) is stored in the network. Test the Hopfield network with missing entries in the first and second components of the stored vector (i.e. [0 0 1 0]).
Given the input vector, x = [1 1 1 -1] (bipolar) and we initialize the weight matrix (wij) as:
![Rendered by QuickLaTeX.com w_{ij} = \sum [s^T(p)t(p)] \\ = \begin{bmatrix} 1 \\ 1 \\ 1 \\ -1 \end{bmatrix} \begin{bmatrix} 1 & 1 & 1 & -1 \end{bmatrix} \\ = \begin{bmatrix} 1 & 1 & 1 & -1 \\ 1 & 1 & 1 & -1 \\ 1 & 1 & 1 & -1 \\ -1 & -1 & -1 & 1 \\\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-088bcaae61e6a077ba13e53e39212cec_l3.png)
and weight matrix with no self-connection is:

As per the question, input vector x with missing entries, x = [0 0 1 0] ([x1 x2 x3 x4]) (binary). Make yi = x = [0 0 1 0] ([y1 y2 y3 y4]). Choosing unit yi (order doesn’t matter) for updating its activation. Take the ith column of the weight matrix for calculation.
(we will do the next steps for all values of yi and check if there is convergence or not)
![Rendered by QuickLaTeX.com y_{in_{1}} = x_1 + \sum_{j = 1}^4 [y_j w_{j1}] \\ = 0\ + \begin{bmatrix} 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} 0 \\ 1 \\ 1 \\ -1 \end{bmatrix} \\ = 0\ + 1 \\ = 1 \\ Applying\ activation,\ y_{in_1} > 0 \implies y_1 = 1 \\ giving\ feedback\ to\ other\ units,\ we\ get \\ y = \begin{bmatrix} 1 & 0 & 1 & 0 \end{bmatrix} \\ which\ is\ not\ equal\ to\ input\ vector\ \\ x = \begin{bmatrix} 1 & 1 & 1 & 0 \end{bmatrix} \\ Hence,\ no\ covergence.](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9ffe38a933dd3a1f4cceed51c261a612_l3.png) ‘
‘
Now for next unit, we will take updated value via feedback. (i.e. y = [1 0 1 0])
![Rendered by QuickLaTeX.com y_{in_{3}} = x_3 + \sum_{j = 1}^4 [y_j w_{j3}] \\ = 1\ + \begin{bmatrix} 1 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 0 \\ -1 \end{bmatrix} \\ = 1\ + 1 \\ = 2 \\ Applying\ activation,\ y_{in_3} > 0 \implies y_3= 1 \\ giving\ feedback\ to\ other\ units,\ we\ get \\ y = \begin{bmatrix} 1 & 0 & 1 & 0 \end{bmatrix} \\ which\ is\ not\ equal\ to\ input\ vector\ \\ x = \begin{bmatrix} 1 & 1 & 1 & 0 \end{bmatrix} \\ Hence,\ no\ covergence.](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7cba982654b3a73538a4e49ae31ccdfa_l3.png)
Now for next unit, we will take updated value via feedback. (i.e. y = [1 0 1 0])
![Rendered by QuickLaTeX.com y_{in_{4}} = x_4 + \sum_{j = 1}^4 [y_j w_{j4}] \\ = 0\ + \begin{bmatrix} 1 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} -1 \\ -1 \\ -1 \\ 0 \end{bmatrix} \\ = 0\ + (-1)\ + (-1) \\ = -2 \\ Applying\ activation,\ y_{in_4} < 0 \implies y_4= 0 \\ giving\ feedback\ to\ other\ units,\ we\ get \\ y = \begin{bmatrix} 1 & 0 & 1 & 0 \end{bmatrix} \\ which\ is\ not\ equal\ to\ input\ vector\ \\ x = \begin{bmatrix} 1 & 1 & 1 & 0 \end{bmatrix} \\ Hence,\ no\ covergence.](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-adf74446abe9e65ccf77f7a1c18ef93e_l3.png)
Now for next unit, we will take updated value via feedback. (i.e. y = [1 0 1 0])
![Rendered by QuickLaTeX.com y_{in_{2}} = x_2 + \sum_{j = 1}^4 [y_j w_{j2}] \\ = 0\ + \begin{bmatrix} 1 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ 1 \\ -1 \end{bmatrix} \\ = 0\ + 1\ + 1 \\ = 2 \\ Applying\ activation,\ y_{in_2} > 0 \implies y_2= 1 \\ giving\ feedback\ to\ other\ units,\ we\ get \\ y = \begin{bmatrix} 1 & 1 & 1 & 0 \end{bmatrix} \\ which\ is\ equal\ to\ input\ vector\ \\ x = \begin{bmatrix} 1 & 1 & 1 & 0 \end{bmatrix} \\ Hence,\ covergence\ with\ vector\ x.](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8ded292a1baadca53ce9cfb1076f93ce_l3.png)
Continuous Hopfield Network
Unlike the discrete Hopfield networks, here the time parameter is treated as a continuous variable. So, instead of getting binary/bipolar outputs, we can obtain values that lie between 0 and 1. It can be used to solve constrained optimization and associative memory problems. The output is defined as:
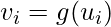
where,
- vi = output from the continuous hopfield network
- ui = internal activity of a node in continuous hopfield network.
Energy Function
The Hopfield networks have an energy function associated with them. It either diminishes or remains unchanged on update (feedback) after every iteration. The energy function for a continuous Hopfield network is defined as:
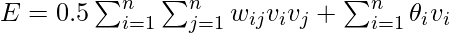
To determine if the network will converge to a stable configuration, we see if the energy function reaches its minimum by:
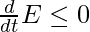
The network is bound to converge if the activity of each neuron wrt time is given by the following differential equation:
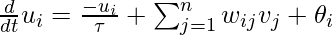
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...