Histogram | Meaning, Example, Types and Steps to Draw
Last Updated :
04 Oct, 2023
What is Histogram?
A histogram is a graphical representation of the frequency distribution of continuous series using rectangles. The x-axis of the graph represents the class interval, and the y-axis shows the various frequencies corresponding to different class intervals. A histogram is a two-dimensional diagram in which the width of the rectangles shows the width of the class intervals, and the length of the rectangles depicts the corresponding frequency.
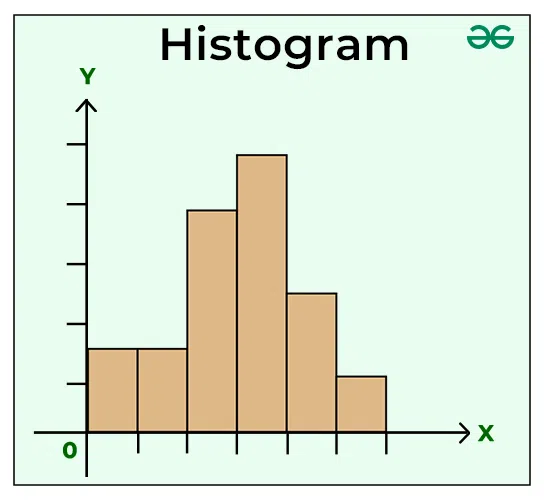
There are no gaps between two consecutive rectangles based on the fact that histograms can be drawn when data are in the form of the frequency distribution of a continuous series. No histogram can be drawn for a data set in the form of discrete series, and this makes histograms different from bar graphs as they can be plotted for both discrete and continuous series. The major difference between a histogram and a bar graph is that the former is two-dimensional; i.e., both the width and length of the rectangles are used for comparison, whereas the latter is one-dimensional, which means only the length of the rectangles is used for comparison. A histogram is used to determine the value of the Mode of a data set in the form of a continuous series.
Types of Histogram
Histograms of Frequency Distribution are of two types:
- Histogram of Equal Class Intervals
- Histogram of Unequal Class Intervals
1. Histogram of Equal Class Intervals
When histograms are drawn based on the data with equal class intervals, they are known as Histograms of equal class intervals. The histogram of equal class intervals includes rectangles with equal width; however, the length of the rectangles is proportional to the frequency distribution of the class intervals.
Example of Histogram of Equal Class Intervals:
Present the following information in the form of a Histogram:
| 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| 16 | 36 | 70 | 50 | 28 |
Solution
- It is visible that the set of data given is of the equal class interval; i.e., the difference between the upper limit and the lower limit of each class interval is 10. So, drawing a Histogram is feasible.
- The X-axis represents the marks (class intervals), and Y-axis represents the number of students (frequency distribution).

2. Histogram of Unequal Class Intervals
When histograms are drawn based on the data with unequal class intervals, they are known as Histograms of unequal class intervals. Histogram of unequal class intervals includes rectangles of different width sizes. Therefore, before drawing a histogram in case of unequal class intervals, frequency distribution has to be adjusted.
Adjustment of frequencies of unequal class intervals:
1. Determine the class of the smallest interval ( lowest class interval ).
2. Then, calculate the adjustment factor using the formula:
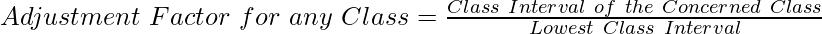
3. Now, adjust the given frequencies using the adjustment factor:
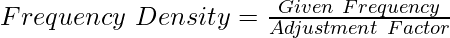
Example of Histogram of Unequal Class Intervals:
Present the following information in the form of a Histogram:
|
10-15
| 14
|
15-20
| 20
|
20-25
| 54
|
25-30
| 30
|
30-40
| 24
|
40-60
| 24
|
60-80
| 16
|
Solution
1. It can be seen clearly that the given class interval is unequal. So, before plotting the histogram, frequencies have to be adjusted.
2. Determine the class of the smallest interval, i.e., 10-15. Thus, the lowest class interval in the given frequency distribution is 5.
3. Formulate the Adjusted Table as shown below:
|
10-15
| 14
| 5 ÷ 5 = 1
| 14 ÷ 1 = 14
|
15-20
| 20
| 5 ÷ 5 = 1
| 20 ÷ 1 = 20
|
20-25
| 54
| 5 ÷ 5 = 1
| 54 ÷ 1 = 54
|
25-30
| 30
| 5 ÷ 5 = 1
| 30 ÷ 1 = 30
|
30-40
| 24
| 10 ÷ 5 = 2
| 24 ÷ 2 = 12
|
40-60
| 24
| 20 ÷ 5 = 4
| 24 ÷ 4 = 6
|
60-80
| 16
| 20 ÷ 5 = 4
| 16 ÷ 4 = 4
|
In the above table, the class interval is calculated as the difference between the upper-class limit and lower-class limit, i.e.,
15-10=5, 20-15=5, 20-25=5, 30-25=5, 40-30=10, 60-40=20, and 80-60=20.
4. Plotting Histogram:

Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...