Higher Order Derivatives are the second, third, or further derivative of the function, i.e. differentiating a function multiple times results in a higher order derivative. Suppose we have a function f(x) then its differentiation is f'(x) which is a first-order derivative. Then its differentiation again f”(x) is called the second order derivative. This is the Higher Order Derivative and then differentiating the second order derivative again results in the third order derivative i.e. f”'(x) is the third derivative of the function f(x) and then higher derivatives are further calculated.
These Higher Order Derivatives are used for various purposes they are used to find the maxima and minima of the function, it is also used for finding the optimal solution of a function, etc.
In this article, we will learn about, Higher Order Derivatives definition, Second Order derivative, Third Order derivative, examples, and others in detail.
Higher Order Derivatives Definition
Derivative of a function tells us about the rate of change of the function. Derivatives are defined using limits and for the function f(x), its derivative is denoted by f'(x). Its definition in terms of limit is given below,
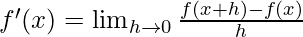
This is also called First Principle and it used to find the derivative of the function. To calculate derivatives for different functions, we usually use the following two properties:
Multiplication Rule for Differentiation
Let’s say we have a complicated function f(x) which is a multiple of two simpler functions h(x) and g(x). In that case, we use the multiplication formula for derivatives.
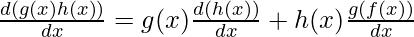
Division Rule for Differentiation
In another case, let’s say our complicated function f(x) is composed to division of two different functions. For example, f(x) = 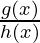
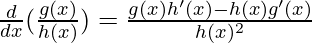
Now, for finding the higher order derivative study the following example, suppose we have a function f(x) then its first order derivative is f'(x) that is found using differentiation formula, then differentiation of f'(x) is again found that is f”(x) is the second order derivative of the function f(x) and then other higher order derivative is found accordingly.
Second Order Derivatives
Second Order Derivative tells us about the rate of change of derivative of a function. It is used to find the maximum and minimum value of a function. It also gives the optimal solution of any equation including functions. We find the second order derivative of any function by further derivating the function.
Let’s say we have a function f(x).
y = f(x)
dy/dx = f'(x)
If f'(x) is differentiable function, we can differentiate it again to get a second-order derivative. It is denoted by,
d/dx{f'(x)} = d2y/dx2
Second Order Derivative are represented as, f”(x).
Example: Given y = x/(x2 + 1). Find the value of second derivative at x = 1
Solution:
Given,
y = x/(x2 + 1)
y’ = 
y’ = 
Now we can differentiate it again to get the second derivative.
y”=
At x = 1
y” = 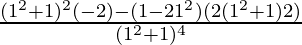
y” = 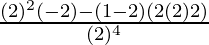
y” = 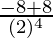
y” = 0
Thus, second order derivative of y = x/(x2 + 1) at x = 1 is, y” = 0.
Third Order Derivative
Third Order Derivative tells us about the rate of change of derivative of second order. We find the third order derivative of any function by further derivating the second order derivative of the function iff differentiation is possible.
Let’s say we have a function f(x).
y = f(x)
dy/dx = f'(x)
If f'(x) is differentiable function, we can differentiate it again to get a second-order derivative. It is denoted by,
f”(x) = d/dx{f'(x)} = d2y/dx2
Differentiating it again with respect to x
d/dx{f”(x)} = d3y/dx3
Third Order Derivative are represented as, f”'(x).
Example: Given y(x) = 3x3 + 12x + 4. Find the value of third derivative at x = 1
Solution:
Given,
y(x) = 3x3 + 12x + 4
Differentiating with respect to x
y'(x) = 3(3x2) + 12(1) + 0
y'(x) = 9x2 + 12 {This first derivative}
Again differentiating with respect to x
y”(x) = 9(2x) + 0
y”(x) = 18x {This second derivative}
Again differentiating with respect to x
y”'(x) = 18(1) = 18 {This required third derivative}
at x = 1
y”'(1) = 18
Higher-Order Derivative in Parametric Form
We can also find higher order derivative of the function in the parametric form. Suppose we are given with functions y(t) and x(t) and they both are the function of parameter ‘t’. Then we can easily find the first order derivative as,
dy/dx = (dy/dt)×(dt/dx)
Now for finding the higher order derivative. Let dy/dt = y'(t) and dx/dt = x'(t) then,
d2y/dx2 = d/dx(dy/dx)
= {d/dt[(dy/dt)×(dt/dx)]}/dx/dt
= d/dt[y'(t)/x'(t)]×dt/dx
Application of Higher Order Derivative
There are various applications of the Higher Order Derivative such as,
- To find the Acceleration of the any length-time function.
- To find maxima and minima of any function
- To find the shape of various graphs.
- For Second Derivative Test, etc.
Read More,
Examples on Higher Order Derivative
Example 1: Given f(x) = x3. Find the value of third derivative of f(x), i.e. f”'(x).
Solution:
f(x) = x3
f'(x) = 3x2
Differentiating it again
f”(x) = 6x
Differentiating it again
f”'(x) = 6
Derivatives
Example 2: Given f(x) = ex + sin(x). Find the value of f”'(x) at x = 0
Solution:
f(x) = ex + sin(x)
First derivative is,
f'(x) = ex + cos(x)
Differentiating it again,
f”(x) = ex – sin(x)
Differentiating it again,
f”'(x) = ex – cos(x)
at x = 0
f”'(0) = e0 – cos (0) = 1 – 1 = 0
f”'(x) = 0
Example 3: Given f(x) = ex.sin(x). Find the value of f”(x) at x = 0.
Solution:
f(x) = ex.sin(x)
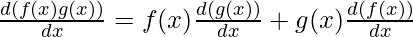
f'(x) = exsin(x) + excos(x)
f'(x) = ex (sin(x) + cos(x))
f”(x) = ex (sin(x) + cos(x)) + ex (cos(x) -sin(x))
f”(x) = ex (2cos(x))
f”(x) = 2excos(x)
at x =0
f”(0) = 2e0cos(0)
f”(0) = 2(1)(1)
f”(0) = 2
Example 4: Given f(x) = ex.sin(x). Find the value of f”(x) at x = 0.
Solution:
f(x) = ex.sin(x)
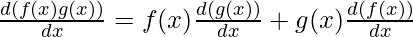
f'(x) = exsin(x) + excos(x)
f'(x) = ex (sin(x) + cos(x))
f”(x) = ex (sin(x) + cos(x)) + ex (cos(x) -sin(x))
f”(x) = ex (2cos(x))
f”(x) = 2excos(x)
Example 5: Given y = 3e2x + 2e3x, prove that 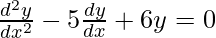
Solution:
y = 3e2x + 2e3x
y’ = 6e2x + 6e3x
y” = 12e2x + 18e3x
Substituting these values in the equation,
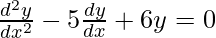
6e2x + 18e3x – 5(6e2x + 6e3x) + 6(3e2x + 2e3x) = 0
12e2x + 18e3x – 30e2x – 30e3x + 18e2x + 12e3x = 0
⇒ 30e2x + 30e3x – 30e2x – 30e3x = 0
⇒ 0 = 0
Hence, Proved.
Example 6: Given y = ex(x + 1). Find the value of second derivative at x = 1.
Solution:
y = ex(x + 1)
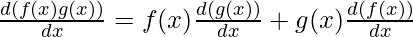
y’ = ex (x + 1) + ex
Now differentiate it again,
y”= 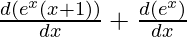
y” = ex (x + 1) + ex + ex
y” = ex(x + 3)
FAQs on Higher-Order Derivatives
1. What is Derivative of a Function?
The derivative of a function is defined as the instantaneus rate of change of a function at any given point. The slope of any curve is also defined using the derivative of the function.
2. What does First Order Derivative of a Function denotes?
First order derivaties of a function gives the instantaneous rate of change of the function at any given point. The first order derivative of a function is given using the first principle.
3. What does Second Order Derivative of a Function denotes?
Second order derivative of a function is given when we differentiate the first order derivative of the function if the first order derivative of the function is a differentiable function.
4. What is Equation for Derivative of the First Order in Parametric Form?
Equation for Derivative of the First Order in Parametric Form is, dy/dx = (dy/dt) × (dt/dx) where t is the parameter
5. What is Equation for Derivative of the Second Order in Parametric Form?
Equation for Derivative of the Second Order in Parametric Form is, d2y/dx2 = (d/dx) (dy/dx) = (d/dt)((dy/dt) × (dt/dx))× (dt/dx) where t is the parameter
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...