Hensel’s Lemma
Last Updated :
07 Jul, 2021
Hensel’s Lemma is a result that stipulates conditions for roots of polynomials modulo powers of primes to be “lifted” to roots modulo higher powers. The lifting method outlined in the proof is reminiscent of Newton’s Method for solving equations. Say the equations of the below type is to be solved:
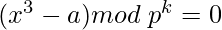
The idea is to use Hensel’s Lemma to solve this type of congruence. It is also known as Hensel’s “lifting” lemma, which is a result of modular arithmetic. If f is a polynomial function and p is a Prime Number, then if f(a1) = 0 (mod p) and [f'(a1)] mod p != 0, then it’s possible to “lift” this solution to the solution for f(x) = 0 (mod pk) by using the below recursion. Note that the [f'(a1)]-1 refers to the modular inverse of f ‘(a1) modulo p.
![Rendered by QuickLaTeX.com a_k + 1 = a_k - f(a_k) * [f'(a_1)]^{-1} (mod \; p^{k+1})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9622ca979ba972b287b11a44786fed05_l3.png)
Example 1:
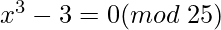
First, solve for (x = 2 is the solution for mod 5)
=> 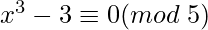
=> 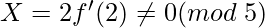
=> ![Rendered by QuickLaTeX.com a_2 = 2 - f(2)[f'(2)]^{-1} mod \; 25](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-076f9632235cd58179425c1ffa270997_l3.png)
=> 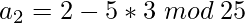
=> 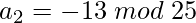
=> 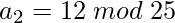
Example 2:
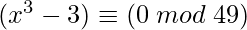
This has no solution as (x3 – 3) % mod 7 = 0 has no solution
Below is the implementation of Hensel’s Lemma:
C++
#include <bits/stdc++.h>
using namespace std;
int inv(int a, int m)
{
int m0 = m, t, q;
int x0 = 0, x1 = 1;
if (m == 1)
return 0;
while (a > 1) {
q = a / m;
t = m;
m = a % m;
a = t;
t = x0;
x0 = x1 - q * x0;
x1 = t;
}
if (x1 < 0)
x1 += m0;
return x1;
}
int derivative(int x)
{
return 3 * x * x;
}
int Image(int x, int k)
{
return x * x * x - k;
}
int next_power(int a_t, int t, int a1,
int prime, int k)
{
int power_p = (int)pow(prime, t + 1);
int next_a = (a_t
- Image(a_t, k)
* inv(derivative(a1),
prime))
% power_p;
if (next_a < 0)
return next_a += power_p;
return next_a;
}
int powerOfPrime(int prime, int power,
int k, int a1)
{
if (derivative(a1) != 0) {
int a_t = a1;
for (int p = 1; p < power; p++) {
a_t = next_power(a_t, p,
a1, prime, k);
}
return a_t;
}
return -1;
}
int main()
{
int prime = 7, a1 = 3;
int power = 2, k = 3;
cout << powerOfPrime(prime, power,
k, a1);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int inv(int a, int m)
{
int m0 = m, t, q;
int x0 = 0, x1 = 1;
if (m == 1)
return 0;
while (a > 1)
{
q = a / m;
t = m;
m = a % m;
a = t;
t = x0;
x0 = x1 - q * x0;
x1 = t;
}
if (x1 < 0)
x1 += m0;
return x1;
}
static int derivative(int x)
{
return 3 * x * x;
}
static int Image(int x, int k)
{
return x * x * x - k;
}
static int next_power(int a_t, int t, int a1,
int prime, int k)
{
int power_p = (int)Math.pow(prime, t + 1);
int next_a = (a_t - Image(a_t, k) *
inv(derivative(a1), prime)) %
power_p;
if (next_a < 0)
return next_a += power_p;
return next_a;
}
static int powerOfPrime(int prime, int power,
int k, int a1)
{
if (derivative(a1) != 0)
{
int a_t = a1;
for(int p = 1; p < power; p++)
{
a_t = next_power(a_t, p,
a1, prime, k);
}
return a_t;
}
return -1;
}
public static void main(String []args)
{
int prime = 7, a1 = 3;
int power = 2, k = 3;
System.out.print(powerOfPrime(prime, power,
k, a1));
}
}
|
Python3
def inv(a, m):
m0 = m
x0 = 0
x1 = 1
if (m == 1):
return 0
while (a > 1):
q = a // m
t = m
m = a % m
a = t
t = x0
x0 = x1 - q * x0
x1 = t
if (x1 < 0):
x1 += m0
return x1
def derivative(x):
return 3 * x * x
def Image(x, k):
return x * x * x - k
def next_power(a_t, t, a1, prime, k):
power_p = int(pow(prime, t + 1))
next_a = (a_t - Image(a_t, k) *
inv(derivative(a1), prime)) % power_p
if (next_a < 0):
next_a += power_p
return next_a
return next_a
def powerOfPrime(prime, power, k, a1):
if (derivative(a1) != 0):
a_t = a1
for p in range(1, power):
a_t = next_power(a_t, p, a1, prime, k)
return a_t
return -1
prime = 7
a1 = 3
power = 2
k = 3
print(powerOfPrime(prime, power, k, a1))
|
C#
using System;
class GFG
{
static int inv(int a, int m)
{
int m0 = m, t, q;
int x0 = 0, x1 = 1;
if (m == 1)
return 0;
while (a > 1)
{
q = a / m;
t = m;
m = a % m;
a = t;
t = x0;
x0 = x1 - q * x0;
x1 = t;
}
if (x1 < 0)
x1 += m0;
return x1;
}
static int derivative(int x)
{
return 3 * x * x;
}
static int Image(int x, int k)
{
return x * x * x - k;
}
static int next_power(int a_t, int t, int a1,
int prime, int k)
{
int power_p = (int)Math.Pow(prime, t + 1);
int next_a = (a_t - Image(a_t, k) *
inv(derivative(a1), prime)) %
power_p;
if (next_a < 0)
return next_a += power_p;
return next_a;
}
static int powerOfPrime(int prime, int power,
int k, int a1)
{
if (derivative(a1) != 0)
{
int a_t = a1;
for(int p = 1; p < power; p++)
{
a_t = next_power(a_t, p,
a1, prime, k);
}
return a_t;
}
return -1;
}
public static void Main(string []args)
{
int prime = 7, a1 = 3;
int power = 2, k = 3;
Console.Write(powerOfPrime(prime, power,
k, a1));
}
}
|
Javascript
<script>
function inv(a, m)
{
let m0 = m, t, q;
let x0 = 0, x1 = 1;
if (m == 1)
return 0;
while (a > 1)
{
q = Math.floor(a / m);
t = m;
m = a % m;
a = t;
t = x0;
x0 = x1 - q * x0;
x1 = t;
}
if (x1 < 0)
x1 += m0;
return x1;
}
function derivative(x)
{
return 3 * x * x;
}
function Image(x, k)
{
return x * x * x - k;
}
function next_power(a_t, t, a1, prime, k)
{
let power_p = Math.floor(Math.pow(prime, t + 1));
let next_a = (a_t - Image(a_t, k) *
inv(derivative(a1), prime)) %
power_p;
if (next_a < 0)
return next_a += power_p;
return next_a;
}
function powerOfPrime(prime, power,
k, a1)
{
if (derivative(a1) != 0)
{
let a_t = a1;
for(let p = 1; p < power; p++)
{
a_t = next_power(a_t, p,
a1, prime, k);
}
return a_t;
}
return -1;
}
let prime = 7, a1 = 3;
let power = 2, k = 3;
document.write(powerOfPrime(prime, power,
k, a1));
</script>
|
Time Complexity: O(log N)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...