Height of a generic tree from parent array

Difficulty Level : Medium
Last Updated : 19 Nov, 2020

We are given a tree of size n as array parent[0..n-1] where every index i in the parent[] represents a node and the value at i represents the immediate parent of that node. For root node value will be -1. Find the height of the generic tree given the parent links.
Examples:

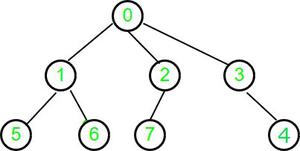
Input : parent[] = {-1, 0, 0, 0, 3, 1, 1, 2}
Output : 2

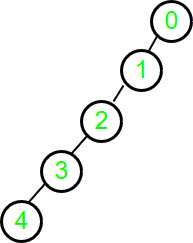
Input  : parent[] = {-1, 0, 1, 2, 3}
Output : 4

Here, a generic tree is sometimes also called an N-ary tree or N-way tree where N denotes the maximum number of child a node can have. In this problem, the array represents n number of nodes in the tree.

Approach 1:
One solution is to traverse up the tree from the node till the root node is reached with node value -1. While Traversing for each node stores maximum path length.
The Time Complexity of this solution is O(n^2).
Approach 2:
Build graph for N-ary Tree in O(n) time and apply BFS on the stored graph in O(n) time and while doing BFS store maximum reached level. This solution does two iterations to find the height of N-ary tree.

C++

// C++ code to find height of N-ary
// tree in O(n)
#include <bits/stdc++.h>
#define MAX 1001
using namespace std;
 
// Adjacency list to
// store N-ary tree
vector<int> adj[MAX];
 
// Build tree in tree in O(n)
int build_tree(int arr[], int n)
{
    int root_index = 0;
 
    // Iterate for all nodes
    for (int i = 0; i < n; i++) {
 
        // if root node, store index
        if (arr[i] == -1)
            root_index = i;
 
        else {
            adj[i].push_back(arr[i]);
            adj[arr[i]].push_back(i);
        }
    }
    return root_index;
}
 
// Applying BFS
int BFS(int start)
{
    // map is used as visited array
    map<int, int> vis;
 
    queue<pair<int, int> > q;
    int max_level_reached = 0;
 
    // height of root node is zero
    q.push({ start, 0 });
 
    // p.first denotes node in adjacency list
    // p.second denotes level of p.first
    pair<int, int> p;
 
    while (!q.empty()) {
 
        p = q.front();
        vis[p.first] = 1;
 
        // store the maximum level reached
        max_level_reached = max(max_level_reached,
                                p.second);
 
        q.pop();
 
        for (int i = 0; i < adj[p.first].size(); i++)
 
            // adding 1 to previous level
            // stored on node p.first
            // which is parent of node adj[p.first][i]
            // if adj[p.first][i] is not visited
            if (!vis[adj[p.first][i]])
                q.push({ adj[p.first][i], p.second + 1 });
    }
 
    return max_level_reached;
}
 
// Driver Function
int main()
{
    // node 0 to node n-1
    int parent[] = { -1, 0, 1, 2, 3 };
 
    // Number of nodes in tree
    int n = sizeof(parent) / sizeof(parent[0]);
 
    int root_index = build_tree(parent, n);
 
    int ma = BFS(root_index);
    cout << "Height of N-ary Tree=" << ma;
    return 0;
}

Python3

# Python3 code to find height 
# of N-ary tree in O(n)
from collections import deque
 
MAX = 1001
 
# Adjacency list to
# store N-ary tree
adj = [[] for i in range(MAX)]
 
# Build tree in tree in O(n)
def build_tree(arr, n):
   
    root_index = 0
 
    # Iterate for all nodes
    for i in range(n):
 
        # if root node, store 
        # index
        if (arr[i] == -1):
            root_index = i
        else:
            adj[i].append(arr[i])
            adj[arr[i]].append(i)
 
    return root_index
 
# Applying BFS
def BFS(start):
   
    # map is used as visited 
    # array
    vis = {}
 
    q = deque()
    max_level_reached = 0
 
    # height of root node is 
    # zero
    q.append([start, 0])
 
    # p.first denotes node in 
    # adjacency list
    # p.second denotes level of 
    # p.first
    p = []
 
    while (len(q) > 0):
        p = q.popleft()
        vis[p[0]] = 1
 
        # store the maximum level 
        # reached
        max_level_reached = max(max_level_reached,
                                p[1])
 
        for i in range(len(adj[p[0]])):
 
            # adding 1 to previous level
            # stored on node p.first
            # which is parent of node 
            # adj[p.first][i]
            # if adj[p.first][i] is not visited
            if (adj[p[0]][i] not in vis ):
                q.append([adj[p[0]][i],
                          p[1] + 1])
 
    return max_level_reached
 
# Driver code
if __name__ == '__main__':
   
    # node 0 to node n-1
    parent = [-1, 0, 1, 2, 3]
 
    # Number of nodes in tree
    n = len(parent)
 
    root_index = build_tree(parent, n)
    ma = BFS(root_index)
    print("Height of N-ary Tree=",
          ma)
 
# This code is contributed by Mohit Kumar 29

Output:

Height of N-ary Tree=4

The Time Complexity of this solution is O(2n) which converges to O(n) for very large n.
Approach 3:
We can find the height of the N-ary Tree in only one iteration. We visit nodes from 0 to n-1 iteratively and mark the unvisited ancestors recursively if they are not visited before till we reach a node which is visited, or we reach the root node. If we reach the visited node while traversing up the tree using parent links, then we use its height and will not go further in recursion.
Explanation For Example 1::

For node 0: Check for Root node is true,
Return 0 as height, Mark node 0 as visited
For node 1: Recur for an immediate ancestor, i.e 0, which is already visited
So, Use its height and return height(node 0) +1
Mark node 1 as visited
For node 2: Recur for an immediate ancestor, i.e 0, which is already visited
So, Use its height and return height(node 0) +1
Mark node 2 as visited
For node 3: Recur for an immediate ancestor, i.e 0, which is already visited
So, Use its height and return height(node 0) +1
Mark node 3 as visited
For node 4: Recur for an immediate ancestor, i.e 3, which is already visited
So, Use its height and return height(node 3) +1
Mark node 3 as visited
For node 5: Recur for an immediate ancestor, i.e 1, which is already visited
So, Use its height and return height(node 1) +1
Mark node 5 as visited
For node 6: Recur for an immediate ancestor, i.e 1, which is already visited
So, Use its height and return height(node 1) +1
Mark node 6 as visited
For node 7: Recur for an immediate ancestor, i.e 2, which is already visited
So, Use its height and return height(node 2) +1
Mark node 7 as visited
Hence, we processed each node in the N-ary tree only once.

C++

// C++ code to find height of N-ary
// tree in O(n) (Efficient Approach)
#include <bits/stdc++.h>
using namespace std;
 
// Recur For Ancestors of node and
// store height of node at last
int fillHeight(int p[], int node, int visited[],
                                   int height[])
{
    // If root node
    if (p[node] == -1) {
 
        // mark root node as visited
        visited[node] = 1;
        return 0;
    }
 
    // If node is already visited
    if (visited[node])
        return height[node];
 
    // Visit node and calculate its height
    visited[node] = 1;
 
    // recur for the parent node
    height[node] = 1 + fillHeight(p, p[node],
                            visited, height);
 
    // return calculated height for node
    return height[node];
}
 
int findHeight(int parent[], int n)
{
    // To store max height
    int ma = 0;
 
    // To check whether or not node is visited before
    int visited[n];
 
    // For Storing Height of node
    int height[n];
 
    memset(visited, 0, sizeof(visited));
    memset(height, 0, sizeof(height));
 
    for (int i = 0; i < n; i++) {
 
        // If not visited before
        if (!visited[i])
            height[i] = fillHeight(parent, i,
                             visited, height);
 
        // store maximum height so far
        ma = max(ma, height[i]);
    }
 
    return ma;
}
 
// Driver Function
int main()
{
    int parent[] = { -1, 0, 0, 0, 3, 1, 1, 2 };
    int n = sizeof(parent) / sizeof(parent[0]);
 
    cout << "Height of N-ary Tree = "
         << findHeight(parent, n);
    return 0;
}

Java

// Java code to find height of N-ary
// tree in O(n) (Efficient Approach)
import java.util.*;
class GFG
{
 
// Recur For Ancestors of node and
// store height of node at last
static int fillHeight(int p[], int node, 
                      int visited[], int height[])
{
    // If root node
    if (p[node] == -1)
    {
 
        // mark root node as visited
        visited[node] = 1;
        return 0;
    }
 
    // If node is already visited
    if (visited[node] == 1)
        return height[node];
 
    // Visit node and calculate its height
    visited[node] = 1;
 
    // recur for the parent node
    height[node] = 1 + fillHeight(p, p[node],
                            visited, height);
 
    // return calculated height for node
    return height[node];
}
 
static int findHeight(int parent[], int n)
{
    // To store max height
    int ma = 0;
 
    // To check whether or not node is visited before
    int []visited = new int[n];
 
    // For Storing Height of node
    int []height = new int[n];
 
    for(int i = 0; i < n; i++)
    {
        visited[i] = 0;
        height[i] = 0;
    }
 
    for (int i = 0; i < n; i++) 
    {
 
        // If not visited before
        if (visited[i] != 1)
         
            height[i] = fillHeight(parent, i,
                            visited, height);
 
        // store maximum height so far
        ma = Math.max(ma, height[i]);
    }
    return ma;
}
 
// Driver Code
public static void main(String[] args) 
{
    int parent[] = { -1, 0, 0, 0, 3, 1, 1, 2 };
    int n = parent.length;
 
    System.out.println("Height of N-ary Tree = " +
                           findHeight(parent, n));
}
}
 
// This code is contributed by 29AjayKumar

Python3

# Python3 code to find height of N-ary 
# tree in O(n) (Efficient Approach) 
 
# Recur For Ancestors of node and 
# store height of node at last 
def fillHeight(p, node, visited, height):
     
    # If root node 
    if (p[node] == -1): 
 
        # mark root node as visited 
        visited[node] = 1
        return 0
 
    # If node is already visited 
    if (visited[node]): 
        return height[node] 
 
    # Visit node and calculate its height 
    visited[node] = 1
 
    # recur for the parent node 
    height[node] = 1 + fillHeight(p, p[node], 
                                  visited, height) 
 
    # return calculated height for node 
    return height[node]
 
def findHeight(parent, n):
     
    # To store max height 
    ma = 0
 
    # To check whether or not node is 
    # visited before 
    visited = [0] * n
 
    # For Storing Height of node 
    height = [0] * n 
 
    for i in range(n):
 
        # If not visited before 
        if (not visited[i]):
            height[i] = fillHeight(parent, i,
                                   visited, height) 
 
        # store maximum height so far 
        ma = max(ma, height[i])
 
    return ma
 
# Driver Code
if __name__ == '__main__':
 
    parent = [-1, 0, 0, 0, 3, 1, 1, 2] 
    n = len(parent)
 
    print("Height of N-ary Tree =",
             findHeight(parent, n))
 
# This code is contributed by PranchalK

C#

// C# code to find height of N-ary
// tree in O(n) (Efficient Approach)
using System;
     
class GFG
{
 
// Recur For Ancestors of node and
// store height of node at last
static int fillHeight(int []p, int node, 
                      int []visited, 
                      int []height)
{
    // If root node
    if (p[node] == -1)
    {
 
        // mark root node as visited
        visited[node] = 1;
        return 0;
    }
 
    // If node is already visited
    if (visited[node] == 1)
        return height[node];
 
    // Visit node and calculate its height
    visited[node] = 1;
 
    // recur for the parent node
    height[node] = 1 + fillHeight(p, p[node],
                            visited, height);
 
    // return calculated height for node
    return height[node];
}
 
static int findHeight(int []parent, int n)
{
    // To store max height
    int ma = 0;
 
    // To check whether or not 
    // node is visited before
    int []visited = new int[n];
 
    // For Storing Height of node
    int []height = new int[n];
 
    for(int i = 0; i < n; i++)
    {
        visited[i] = 0;
        height[i] = 0;
    }
 
    for (int i = 0; i < n; i++) 
    {
 
        // If not visited before
        if (visited[i] != 1)
         
            height[i] = fillHeight(parent, i,
                            visited, height);
 
        // store maximum height so far
        ma = Math.Max(ma, height[i]);
    }
    return ma;
}
 
// Driver Code
public static void Main(String[] args) 
{
    int []parent = { -1, 0, 0, 0, 3, 1, 1, 2 };
    int n = parent.Length;
 
    Console.WriteLine("Height of N-ary Tree = " +
                          findHeight(parent, n));
}
}
 
// This code contributed by Rajput-Ji

Output:

Height of N-ary Tree = 2

Time Complexity: O(n)

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready.

My Personal Notes

Related Articles

C++

Python3

C++

Java

Python3

C#