Heating Effect of Electric Current is a phenomenon that is generally used in our daily life. The electric kettle, toaster, heater, and other appliances are utilized as alternates for traditional cooking and laundry methods. Electric bulbs, which are an alternative to conventional lighting, utilize the same concept. Over time, these technologies have revolutionized the world. Conductors or Wires produce heat energy when a current pass through them. This is because of the fact that when an electric current passes through it, fast electron collisions start to occur. This concept or phenomenon is known as the Heating Effect of Electric Current. Hence, the idea of the heating effect of electric current and its applications will be covered in this article in detail!
What is the Heating Effect of Electric Current?
When an electric current is allowed to flow through a high resistance wire, such as nichrome wire, the conductor heats up and produces heat. Such a heating action of a conductor is known as the Heating effect of Current.
When we use some electrical appliances, the chemical reactions which occur in the cells on which they run generate some potential difference between its terminals which sets the electrons in motion. To maintain the flow of current the source needs to expand some energy. A part of the energy is used in doing some sort of useful work like moving the fan blades in case of electricity-generated fans, etc. The remaining energy is exploited or expanded in the form of heat which raises the temperature of the appliance. If we are using a circuit in an appliance that is purely resistive then a lot of energy is dissipated entirely in the form of what we call heat. This is called or known as the heating effect of electric current.
Effects of Heat on the Conductor
- The heating effect may cause an increase in the temperature of the wire of the conductor.
- This may also cause an increase in the volume of the material.
More simply, when an electrical current is passed through a conductor, it generates excess heat due to the resistance caused by the electrons in the conductor to the flowing current. The work done in overcoming this resistance to the current generates what we call heat in that conductor. The electrical heating effect of the electrical current is most commonly and widely applied and used in our daily life. For example, electrical irons, kettles, toasters, electrical heaters, etc. are used widely as alternatives to conventional methods of cooking and also laundry. This same effect is used widely in electrical bulbs which are alternatives to conventional incandescent lamps. These devices have modernized and revolutionized the new sustainable world over the years.
Heating Effect of Electric Current Formula
Let us assume a current I that is flowing through a resistor that has a resistance of R as shown in the circuit. Let the potential difference across ends of the terminals of the battery be V. Let us assume to be the time during which a charge of Q amount flows across the circuit. The work which is done in moving that charge Q through a potential difference V is V × I.
Hence, the source has to supply energy equal to V × I in time t. Therefore, the power input to the electrical circuit by the source is
P = V × Q/t
= V × I
Or the energy that is being supplied to the circuit by the source in time t is P × t, that is, V × I × t. This extra energy generated gets dissipated in the resistor in the form of heat. Therefore, for a steady and fixed current I, the amount of heat denoted by H that is produced in time t is
H = V × I × t
Joules Law of Heating
The very famous physicist James Prescott found that the amount of heat generated per second that develops in a conductor having a current is directly proportional to the electrical resistance of the wire and also with the square of the current given. This heat which is liberated or generated because of the electrical current that flows in an electrical wire is expressed in Joules.
By applying the ohms law to the equation H = V × I × t. We can deduce the Joules law or joules first law which gives the relationship between the heat that is produced by flowing charges of electric current through a conductor. It is directly proportional to the square of the supplied current, the electrical resistance exerted by the appliance, and the time for which we used it. This is known or called joule’s law of heating. The following is its expression:
H = I2 × R × t
where,
- H gives or indicates the amount of heat.
- I shows the amount ofthe electrical current supplied.
- R is the value or amount of electric resistance exerted in the conductor.
- t denotes the time for which the appliance is operated.
Factors on which Heat Depends
- The amount of liberated or generated heat is directly proportional to the given wire’s electrical resistance when the electrical current in the given circuit and the flow of supplied current is not altered or changed.
- The amount of liberated or generated heat in the conductor carrying current is directly proportional to the square of the electrical current that flows through the given circuit when the electrical resistance and current supply is kept constant.
- The amount of heat generated or produced because of the electrical current flow is directly proportional to the time of usage of flow when the electrical resistance and the current flow is constant.
Applications of Heating Effect of Electric Current
Following are some of the widely used common devices in which the heating effect of current is used and harnessed for other purposes:
Electric Fuse
In any electrical instrument which we sometimes use due to a sudden rise in the amount of current, the instrument or appliance gets overheated or burnt down which sometimes may result in a severe fire. A conducting wire with a very low melting point is joined or connected in a series connection with the device or appliance circuit to avoid any mishap or this type of accident. Whenever the current value somehow accidentally rises, the wire inside the fuse melts due to the excessive heating and thus results in breaking the electrical circuit saving the device as well as our lives. We choose or select the fuse according to the appliance used. A device or an appliance that works on a higher current needs a greater value of fuse and vice versa.
Electric Bulb
Electrical bulb contains a very thick metallic wire which is in turn made up of highly resistive tungsten metal. This metal is always kept in an inert environment so that it doesn’t react with a neutral gas or vacuum. When the electrical current flows through the used tungsten wire, it becomes warm or heated, and then it emits light. Most of the electrical power which is drawn in the electrical circuit from the electrical source is liberated or dissipated in the form of heat and the rest is given or emitted in the form of light energy. The tungsten filament used also has a high resistivity and a very high melting point so that it doesn’t get heated easily when used.
Electric Heater
In an electrical heater, a very high resistance nichrome wire is mostly and commonly used as a coil. The coil is rotated or wound on grooves which are made up of the ceramic material of the iron plate or china clay plate. Whenever the electrical current flows in the coil, it quickly becomes warm or heated, which is then widely used to heat our cooking vessels. In mountain areas, electrical room heaters are used to keep their rooms warm and heated to save themselves from the exhaustive cold outside.
Electric Iron
Between the metal part and the electrical coil in an iron, Mica is placed which is by nature an insulator. The coil of the iron becomes warm or heated with the continuous passage of current which is then passed on or transferred to the metallic part through the mica used. Finally, after a while, the metallic part becomes very heated or whatever temperature we have set, which is then used for ironing different material clothes according to our wish.
For using and harnessing the heating effect of electric current, the element of appliances needs or is required to have a high melting point to retain more heat.
Solved Examples on Heating Effect of Electric Current
Example 1: 100 J of heat energy is produced by an electrical appliance that is used for 1 sec and is having a resistance of 4 ohms. Find and calculate the potential difference of the appliance.
Solution:
As we know,
H = I2×R×t
Given, H = 100 J, R = 4 ohm, t = 1 sec
Therefore, 100J=I2×4×1
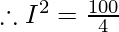
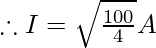
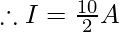
I = 5 A
From ohm’s law we know
V=I×R
Therefore, V = 5A × 4Ω
V = 20 V
Therefore, the potential difference generated is 20 V.
Example 2: Find out the heat produced by the electric toaster when it is used for 5 minutes. The current given was 2 A and its resistance is 3 ohms.
Solution:
As we know,
H = I2×R×t
Given, I = 2 A, R = 3 ohm, t = 5 min = 300 sec
Therefore, H=22×3×300J
H = 22×900 J
Therefore, H=4×900 J
H = 3600 J
Hence, the heat that is produced or liberated by the electrical toaster is 3600 J.
Example 3: The heat generated is 100 J from an electrical fan which has a potential difference of 10 V and the time for which it is used is 10 sec. Find what the amount of electrical current that is used is?
Solution:
As we know,
H = V × I × t
Given, H = 100 J, V = 10 V, t = 10 sec
Therefore, 100J=10V×I×10
∴100J = 100 × I
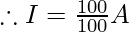
I = 1 A.
Therefore, the current used is 1 A.
Example 4: What is the power consumed if a device or appliance is operated at 1 V potential difference and 6 A current?
Solution:
As we know,
P = V × I
Given, V = 1V AND I = 6 A
P = 1 V × 6 A
P = 6 W
Hence, the power that has been consumed is 6 W.
Example 5: What is the power consumed if a toaster having 3-ohm resistance is operated at 1 A current?
Solution:
As we know,
P = I2 × R
Given, I = 1 A and R = 3 ohm
∴P = 12 × 3Ω
P = 3 W.
Therefore, the power consumed has been calculated to be 3 W.
FAQs on Heating Effect of Electric Current
Question 1: What is the Heating Effect of Electric Current?
Answer:
A high resistance wire, such as nichrome wire, heats up and emits heat when an electrical current is carried through it. The heating action of current is what causes the Heating effect of Current.
Question 2: Name two Appliances based on the Heating Effect of Electric Current.
Answer:
Two appliance that work on the principle of Heating Effect of Electric Current are Electric Fuse and Electric Iron.
Question 3: Mention two Practical Disadvantages of the Heating Effect of Electric Current.
Answer:
Two Practical Disadvantages of the Heating Effect of Electric Current are:
- A part of the electrical current that travels through the conductor is transformed to heat. Often, this is a waste of energy.
- The heat generated can start a fire or harm the insulation and other electrical parts.
Question 4: Write a common example of the Heating Effect of an Electric Current.
Answer:
Electrolysis is an important and common example of the heating effect of electric current.
Question 5: What is the Heating Effect of the Electric Current Formula?
Answer:
The Heating Effect of Electric Current Formula is given by,
H = I2 × R × t
where,
- H gives or indicates the amount of heat.
- I shows the amount ofthe electrical current supplied.
- R is the value or amount of electric resistance exerted in the conductor.
- t denotes the time for which the appliance is operated.
Related Articles
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...