Handshaking Lemma and Interesting Tree Properties
Last Updated :
21 Jul, 2023
Introduction
Trees are an important concept in graph theory, and understanding their properties is crucial in solving many graph-related problems. In this article, we will explore two important properties of trees – the Handshaking Lemma and interesting tree properties.
What is Handshaking Lemma?
Handshaking lemma is about an undirected graph. In every finite undirected graph, an even number of vertices will always have an odd degree. The handshaking lemma is a consequence of the degree sum formula (also sometimes called the handshaking lemma)
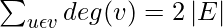
To understand the Handshaking Lemma, let’s consider an example. Suppose we have a tree with n vertices and n-1 edges. The Handshaking Lemma states that the sum of the degrees of all the vertices in this tree is 2(n-1).
To prove the Handshaking Lemma, we can use the fact that each edge connects two vertices, so it contributes 2 to the sum of the degrees of all vertices. Thus, the total sum of the degrees of all vertices is equal to twice the number of edges.
The Handshaking Lemma is a useful tool in solving graph-related problems. For example, it can be used to determine whether a graph has an Eulerian path or cycle. An Eulerian path is a path that visits every edge of a graph exactly once, while an Eulerian cycle is a cycle that visits every vertex of a graph exactly once. If a graph has an Eulerian path or cycle, then the sum of the degrees of all vertices must be even.
How is Handshaking Lemma useful in Tree Data structure?
Following are some interesting facts that can be proved using the Handshaking lemma.
1) In a k-ary tree where every node has either 0 or k children, the following property is always true.
L = (k - 1)*I + 1
Where L = Number of leaf nodes
I = Number of internal nodes
Proof:
Proof can be divided into two cases.
- Case 1 (Root is Leaf): There is only one node in the tree. The above formula is true for a single node as L = 1, I = 0.
- Case 2 (Root is Internal Node): For trees with more than 1 node, the root is always an internal node. The above formula can be proved using Handshaking Lemma for this case. A tree is an undirected acyclic graph.
Total number of edges in Tree is number of nodes minus 1, i.e., |E| = L + I – 1.
All internal nodes except root in the given type of tree have degree k + 1. Root has a degree k. All leaves have degree 1. Applying the Handshaking lemma to such trees, we get the following relation.
Sum of all degrees = 2 * (Sum of Edges)
Sum of degrees of leaves +
Sum of degrees for Internal Node except root +
Root's degree = 2 * (No. of nodes - 1)
Putting values of above terms,
L + (I-1)*(k+1) + k = 2 * (L + I - 1)
L + k*I - k + I -1 + k = 2*L + 2I - 2
L + K*I + I - 1 = 2*L + 2*I - 2
K*I + 1 - I = L
(K-1)*I + 1 = L
So the above property is proved using Handshaking Lemma, let us discuss one more interesting property.
Alternate Proof: (Without using Handshaking Theorem):
Since there are I internal nodes, each having K children, therefore total children in the tree = K * I.
There are I-1 internal nodes that are children of some other node (root has been excluded hence one less than the total number of internal nodes)
That is, out of these K*I children, I-1 are internal nodes and therefore the rest (K*I – (I-1)) are leaves.
Hence L = (K-1)*I + 1.
2) In a Binary tree, the number of leaf nodes is always one more than nodes with two children.
L = T + 1
Where L = Number of leaf nodes
T = Number of internal nodes with two children
Proof:
Let a number of nodes with 2 children are T. Proof can be divided into three cases.
Case 1: There is only one node, the relationship holds
as T = 0, L = 1.
Case 2: Root has two children, i.e., the degree of the root is 2.
Sum of degrees of nodes with two children except root +
Sum of degrees of nodes with one child +
Sum of degrees of leaves + Root's degree = 2 * (No. of Nodes - 1)
Putting values of above terms,
(T-1)*3 + S*2 + L + 2 = (S + T + L - 1)*2
Cancelling 2S from both sides.
(T-1)*3 + L + 2 = (T + L - 1)*2
T - 1 = L - 2
T = L - 1
Case 3: Root has one child, i.e., the degree of the root is 1.
Sum of degrees of nodes with two children +
Sum of degrees of nodes with one child except root +
Sum of degrees of leaves + Root's degree = 2 * (No. of Nodes - 1)
Putting values of above terms,
T*3 + (S-1)*2 + L + 1 = (S + T + L - 1)*2
Cancelling 2S from both sides.
3*T + L -1 = 2*T + 2*L - 2
T - 1 = L - 2
T = L - 1
Therefore, in all three cases, we get T = L-1.
We have discussed proof of two important properties of Trees using Handshaking Lemma. Many GATE questions have been asked on these properties, the following are a few links.
GATE-CS-2015 (Set 3) | Question 35
GATE-CS-2015 (Set 2) | Question 20
GATE-CS-2005 | Question 36
GATE-CS-2002 | Question 34
GATE-CS-2007 | Question 43
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...