Hamming Code in Computer Network
Last Updated :
12 Apr, 2024
Hamming code is a set of error-correction codes that can be used to detect and correct the errors that can occur when the data is moved or stored from the sender to the receiver. It is a technique developed by R.W. Hamming for error correction.
What is Redundant Bits?
Redundant bits are extra binary bits that are generated and added to the information-carrying bits of data transfer to ensure that no bits were lost during the data transfer. The number of redundant bits can be calculated using the following formula:
2^r ≥ m + r + 1
Suppose the number of data bits is 7, then the number of redundant bits can be calculated using: = 2^4 ≥ 7 + 4 + 1 .Thus, the number of redundant bits= 4
Types of Parity bits
A parity bit is a bit appended to a data of binary bits to ensure that the total number of 1’s in the data is even or odd. Parity bits are used for error detection. There are two types of parity bits:
- Even parity bit: In the case of even parity, for a given set of bits, the number of 1’s are counted. If that count is odd, the parity bit value is set to 1, making the total count of occurrences of 1’s an even number. If the total number of 1’s in a given set of bits is already even, the parity bit’s value is 0.
- Odd Parity bit: In the case of odd parity, for a given set of bits, the number of 1’s are counted. If that count is even, the parity bit value is set to 1, making the total count of occurrences of 1’s an odd number. If the total number of 1’s in a given set of bits is already odd, the parity bit’s value is 0.
Algorithm of Hamming Code
Hamming Code is simply the use of extra parity bits to allow the identification of an error.
- Write the bit positions starting from 1 in binary form (1, 10, 11, 100, etc).
- All the bit positions that are a power of 2 are marked as parity bits (1, 2, 4, 8, etc).
- All the other bit positions are marked as data bits.
- Each data bit is included in a unique set of parity bits, as determined its bit position in binary form. a. Parity bit 1 covers all the bits positions whose binary representation includes a 1 in the least significant position (1, 3, 5, 7, 9, 11, etc). b. Parity bit 2 covers all the bits positions whose binary representation includes a 1 in the second position from the least significant bit (2, 3, 6, 7, 10, 11, etc). c. Parity bit 4 covers all the bits positions whose binary representation includes a 1 in the third position from the least significant bit (4–7, 12–15, 20–23, etc). d. Parity bit 8 covers all the bits positions whose binary representation includes a 1 in the fourth position from the least significant bit bits (8–15, 24–31, 40–47, etc). e. In general, each parity bit covers all bits where the bitwise AND of the parity position and the bit position is non-zero.
- Since we check for even parity set a parity bit to 1 if the total number of ones in the positions it checks is odd.
- Set a parity bit to 0 if the total number of ones in the positions it checks is even.

Determining the Position of Redundant Bits
A redundancy bits are placed at positions that correspond to the power of 2. As in the above example:
- The number of data bits = 7
- The number of redundant bits = 4
- The total number of bits = 7+4=>11
- The redundant bits are placed at positions corresponding to power of 2- 1, 2, 4, and 8

- Suppose the data to be transmitted is 1011001 from sender to receiver, the bits will be placed as follows:

Determining the Parity bits According to Even Parity
- R1 bit is calculated using parity check at all the bits positions whose binary representation includes a 1 in the least significant position. R1: bits 1, 3, 5, 7, 9, 11
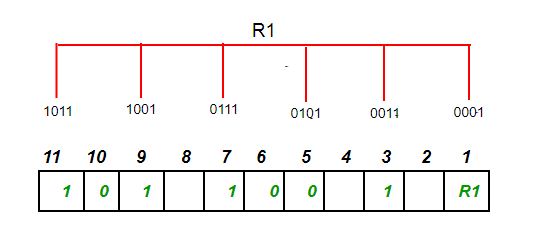
- To find the redundant bit R1, we check for even parity. Since the total number of 1’s in all the bit positions corresponding to R1 is a odd number the value of R1 (parity bit’s value) = 1
- R2 bit is calculated using parity check at all the bits positions whose binary representation includes a 1 in the second position from the least significant bit. R2: bits 2,3,6,7,10,11

- To find the redundant bit R2, we check for even parity. Since the total number of 1’s in all the bit positions corresponding to R2 is odd the value of R2(parity bit’s value)=1
- R4 bit is calculated using parity check at all the bits positions whose binary representation includes a 1 in the third position from the least significant bit. R4: bits 4, 5, 6, 7

- To find the redundant bit R4, we check for even parity. Since the total number of 1’s in all the bit positions corresponding to R4 is an even the value of R4(parity bit’s value) = 0
- R8 bit is calculated using parity check at all the bits positions whose binary representation includes a 1 in the fourth position from the least significant bit. R8: bit 8,9,10,11

- To find the redundant bit R8, we check for even parity. Since the total number of 1’s in all the bit positions corresponding to R8 is an even number the value of R8(parity bit’s value)=0. Thus, the data transferred is:

Error Detection and Correction
Suppose in the above example the 6th bit is changed from 0 to 1 during data transmission, then it gives new parity values in the binary number:

For all the parity bits we will check the number of 1’s in their respective bit positions.
- For R1: bits 1, 3, 5, 7, 9, 11. We can see that the number of 1’s in these bit positions are 4 and that’s even so we get a 0 for this.
- For R2: bits 2,3,6,7,10,11 . We can see that the number of 1’s in these bit positions are 5 and that’s odd so we get a 1 for this.
- For R4: bits 4, 5, 6, 7 . We can see that the number of 1’s in these bit positions are 3 and that’s odd so we get a 1 for this.
- For R8: bit 8,9,10,11 . We can see that the number of 1’s in these bit positions are 2 and that’s even so we get a 0 for this.
- The bits give the binary number 0110 whose decimal representation is 6. Thus, bit 6 contains an error. To correct the error the 6th bit is changed from 1 to 0.
Features of Hamming Code
Error Detection and Correction: Hamming code is designed to detect and correct single-bit errors that may occur during the transmission of data. This ensures that the recipient receives the same data that was transmitted by the sender.
Redundancy: Hamming code uses redundant bits to add additional information to the data being transmitted. This redundancy allows the recipient to detect and correct errors that may have occurred during transmission.
Efficiency: Hamming code is a relatively simple and efficient error-correction technique that does not require a lot of computational resources. This makes it ideal for use in low-power and low-bandwidth communication networks.
Widely Used: Hamming code is a widely used error-correction technique and is used in a variety of applications, including telecommunications, computer networks, and data storage systems.
Single Error Correction: Hamming code is capable of correcting a single-bit error, which makes it ideal for use in applications where errors are likely to occur due to external factors such as electromagnetic interference.
Limited Multiple Error Correction: Hamming code can only correct a limited number of multiple errors. In applications where multiple errors are likely to occur, more advanced error-correction techniques may be required.
For Implementation you can refer this article.
Question on Hamming Code
Q.1: Assume that 12 bit hamming codeword consist of 8 bit data and 4 check bits is d8d7d6d5c4d4d3d2c3d1c2c1 ,where the data bits and the check bits are given in the following tables: [GATE 2021 ]

Which one of the following choices gives the correct values of x and y ?
(A) x is 0 and y is 0
(B) x is 0 and y is 1
(C) x is 1 and y is 0
(D) x is 1 and y is 1
Answer: (A)
We will first insert our codeword according to hamming code d8d7d6d5c4d4d3d2c3d1c2c1,
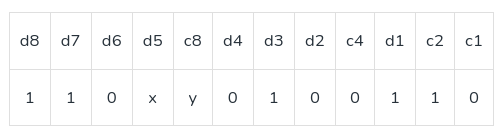
Now,calculating hamming code according to first parity bit C1: d7d5d4d2d1c1. 1×0010, To make number of 1 even , for this x must be 0.
Similarly, lets calculate for y , we will start from c8 and make its even=>110xy here x is already 0 , so y should be 0.
So the value of x is 0 and y is 0.
For more details you can refer GATE | GATE CS 2021 | Set 1 | Question 39 published quiz.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...