Grouped Convolution

The convolution neural network is very helpful in reducing the parameter while training the image dataset as compared to ANN, which makes it nearly impossible to train medium size images. The method that is useful in reducing parameters in convents called filter grouping. 

Grouped convolution was first introduced in 2012 in the AlexNet paper. The main idea behind this method to use the limited memory of two GPUs of 1.5 GB each to train the model in parallel. Incidentally, the memory required by the model to train is just under 3GB.

First, let’s discussed some other reasons why grouped convolution is required:

• In order to obtain good training and testing accuracy on various Image datasets, we need to build a deep neural network with multiple kernels per layer that lead to multiple channels per layer. This resulted in a wider neural network.
• Each kernel filter convolves on all the feature maps obtained on the previous layer, resulting in lots of convolutions, some of which may be redundant.
• Training deeper models will be hard because fitting these models on a single GPU wouldn’t be easy. Even if it were possible, we might have to use a smaller batch size which would make the overall convergence difficult.

From the above points, we can say that filter grouping is an important aspect in decreasing the complexity of CNN and thus facilitating the training of the larger neural networks.

Architecture and Working

Below is the sample representative of the grouped convolution.

In filter groups, we take into account the channel dimension i.e the third dimension of convolution filter, as we go deeper into the convolution this dimension increases very rapidly thus increases complexity. The spatial dimensions have some degree of effect on the complexity but in deeper layers, they are not really the cause of concern. Thus in bigger neural networks, the filter groups will dominate.

Image depicting filter grouping by dividing the number of channels to half

In the above figure, we can see that convolution with 2 filter groups that are created from one, each of the 2 filter groups convolves with only half of the channel dimension of the previous layer. There are different variants of the division of filter groups one such variation is the logarithmic filter factorization.

Logarithmic Factorization

This method was proposed by the researchers of KAIST Korea in the paper titled ‘Convolution with Logarithmic Filter Groups for Efficient Shallow CNN’.  They use non-linear logarithmic filter grouping and argue that it is based on the non-linear characteristic of filters. To support their claims they used the Weber-Fechner law. This law states that the degree of subjective sensation is proportional to the logarithm of the stimulus intensity, and it can be used to explain auditory and visual systems in humans.

Logarithmic filter convolution

The proposed nonlinear filter grouping uses logarithmic scales with base 2 to decide the size of each filter group in a convolution layer. 

Let’s consider a convolution layer that has input and output channel depth of c_in and c_out. If the number of filter groups is n, then the set of filter shapes of a convolution layer with the logarithmic filter grouping would be :

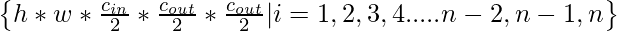
The authors also used residual identity connection between input and output of the grouped convolution layer in order to build sufficient shallow networks. Below is the architecture for it:

Logarithmic Filter convolution with residual identity connection

Conclusion:

• The proposed method of filter grouping allows us to build a sufficiently deep & wide neural network by replicating the grouped convolution.
• If not for filter grouping, the complexity of the network increases exponentially as we go into deeper layers.
• The filter grouping also helped to facilitate the parallelism in the model.

References:

• Logarithmic Filter Groups paper 
• Deep Net paper