GRE Data Analysis | Counting Methods

Counting is the process of determining the number of elements of a finite set of objects. If set contains small number of objects/elements then it is easy to list and count them. When the set is too large to count that way, and when the objects are related in a patterned or systematic way, there are some useful techniques for counting the objects without actually listing them.

1. Sets:

A set is defined as a well defined unordered collection of distinct elements or objects. It is a collection of elements that have some property. Example: 

A = { 0, 2, 4, 6, 8 }
B = { 1, 2, 3, 4, 5, 6......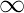 }C = set of all students in a class 

For any finite set S, the number of elements of set S is represented by |S| Thus, in above example |A| = 5 and also 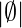= 0, where 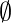is empty set. Set operations

2. Lists:

A list is a data structure consisting of an ordered set of elements. It is like a finite set. 

Difference between lists and sets:

1. Elements can be repeated in a list but in set elements are distinct.
2. Rearranging the members of the list makes it a different list, hence members of list are ordered.

Thus, list 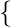1, 2, 3, 4 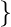and list 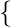4, 2, 3, 1 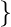are different. Inclusion-Exclusion Principle: It states that the number of elements in the union of two sets equals the sum of their individual numbers of elements minus the number of elements in their intersection. Let say we have finite Sets A and B then

  =    +    + 

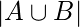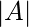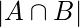
If A and B are mutually exclusive then, A B = 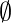. Then,

  =    +  

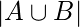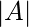3. Multiplication Principle:

Multiplication principle states that if one event can occur in m ways and a second can occur independently of the first in n ways, then the two events can occur in m*n ways. 

Example: A computer password consists of four characters such that the first character is one of the 10 digits from 0 to 9 and each of the next 3 characters is any one of the uppercase letters from the 26 letters of the English alphabet. How many different passwords are possible? Explanation: First character can take one of the 10 values and next characters can take one of the 26 values, we have 10 choices for first character 26 for the second, third and fourth character the total number of possible passwords are,

10*26*26*26 =  175,760 

Let say repetitions of the letters not allowed then the choices are not all independent but we can apply a modification of the multiplication principle, here we have 10 choices for first character, 26 choices for second character, 25 choices for third character, 24 choices for fourth character. The total number of possible passwords are,

10*26*25*24 = 156, 000 

4. Factorials:

It is used for counting, denoted as 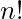. 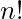is the product of first n natural numbers.

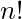 = 1*2*3*4......(n-1)*n

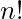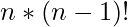= [Tex]4!    [/Tex]= 1*2*3*4 = 24 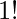= 1 = 1; 

Example: Determine the number of different ways the 3 letters A, B and C can be placed in order from 1st to 3rd. 

Explanation: Letters A, B and C can be arranged in 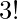= 6 ways

ABC  ACB  BAC  BCA  CAB  CBA

it can also be understand that in first place we can put 3 letters in second there is only 2 choices left in 3rd place only one choice left so, 3*2*1 = 6.

5. Permutation and Combination:

Permutation: Permutation refers to the arrangement, Permutation of n object taking r at a time is given as

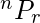  =  n*(n-1)*(n-2)*(n-3)...(n-r+1)  =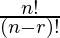  

Example: How many different 5-digit positive integers can be formed using the digits 1, 2, 3, 4, 5, 6, and 7 if none of the digits can occur more than once in the integer? 

Explanation: Total number of 5 digit positive integers that can be formed using the 7 digits is: 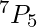= = 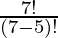7*6*5*4*3 It can also be understand that for first place we have 7 choices for second place we have 6 and so on. I.e., total 5-digit positive integers is 7*6*5*4*3 . Combination: A combination is a selection of items from a collection, such that the order of selection does not matter combination of n object taken r at a time is given by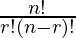 

  =  

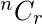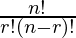
Example: Given 5 letters A, B, C, D and E determine the number of ways in which we can select 3 of the 5 letters. 

Explanation: number of ways of selecting 3 letters of the 5 is 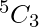, 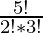= 5*2 = 10 ways

  ABC  ABD  ABE  ACD  ACE  ADE  BCD  BCE  BDE  CDE

If we count the different orders or number of arrangement then, number of ways to select with order = (number of ways to select without order) x (number of ways to order them) hence, for above example there are 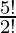= 60 ways. Problems on permutation and combination