GRE Algebra | Solving Quadratic Equations
Last Updated :
25 Apr, 2019
In algebra, a quadratic equation can be written in the form:
ax2 + bx + c = 0
where x is the variable and a, b, c are the real numbers and a≠0. If a=0 then it will be a linear equation not quadratic because no second order term.
If quadratic equation has solution then it can be found by using the
quadratic formula.
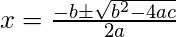
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...