The energy possessed by objects due to changes in their position in a gravitational field is called Gravitational Potential Energy. It is the energy of the object due to the gravitational forces. The work done per unit mass to bring the body from infinity to a location inside the gravitational field of any object is known as gravitational potential and the energy change here is called Gravitational Potential Energy. Let’s learn about Gravitational Potential Energy in detail in this article.
What is Gravitational Potential Energy?
Gravitational Potential Energy is described as the energy of a body that arises from the gravitational force, that is when the gravitational force acts on a body and that force produces a type of potential energy known as gravitational potential energy. Now, if the position changes due to force, the amount of work done on the body by the force is the change in potential energy.
Assume we have two items, one A and the other B. Now, suppose B’s location changes exclusively as a result of a certain force. Assume M’s location is changing owing to gravitational force, followed by a change in potential energy. The quantity of work done by the gravitational force is equal to the change in the location of the item.
As a result, the work done by the gravitational force will be equal to the change in potential energy going through from P to Q. Assume P is position 1 and Q is position 2. In this instance, the effort required to move the item from position 1 to position 2 is equal to the change in potential energy, which is equal to the potential energy at point 2 minus the potential energy at point 1.
The image given below shows the gravitational potential energy of the Earth with respect to the Sun.
Unit and Dimension of Gravitational Potential Energy
Gravitational Potential Energy is represented by the symbol U.
Its SI unit is J/kg.
The dimensional formula of Gravitational Potential Energy is [M1L2T-2]
Gravitational Potential Energy Formula
Mathematically, Gravitational Potential Energy is given by the product of the mass (m) of the object, acceleration due to gravity (g), and height (h) above the ground as
Gravitational Potential Energy,
V = mgh
where,
m is the mass of the object
g is the gravity of the Earth
h is the height at which object is held
Gravitational Potential Energy is negative when mass from infinity approaches the gravitational field of a planet.
The work done on a body is represented by expression when it is elevated to a height from the earth’s surface.
W = mgh
where
m is the mass of the body
The work done on a body when it is in the ground label is zero since its height is zero.
W = 0, at h = 0
Because a body’s height is 0 while it is in the ground label, the work done on it is zero.
When a force is applied to a body, it changes its position. The amount of work done on the body equals the change in the potential energy of the body. Consider a body that has been transported vertically from a point at height h1 to a position at height h2. The work done by the force put on it while raising it via the height between the two places is equal to the difference in gravitational potential energy at this moment.
W = mgh2 – mgh1
Derivation of Gravitational Potential Energy
When a particle is transported over an infinitely short distance, dr. The work done on the second particle by the gravitational force is represented by -Fdr.
dW = -Fdr……(1)
where F is the Gravitational force acting on the particles and is given by,
F = G m1 m2 / r2
where G is the Gravitational constant, m1, and m2 are the masses of the two particles in contact respectively.
On substituting F in equation (1), we get,
dW = -(G m1 m2) dr / r2……(2)
The negative sign in the equation comes from the fact that the displacement is in the opposite direction as the force. The change in gravitational potential energy of the two-particle system during this short movement is equal to the negative work done on the second particle by definition. When a particle is transported over an infinitely short distance, dr.
The work done on the second particle by the gravitational force is denoted by – Fdr.
dU = -dW
= (G m1 m2) dr / r2……(3)
As the second particle goes from B to C, the change in gravitational potential energy of the two-particle system is a function of distance r, and is represented by,
![Rendered by QuickLaTeX.com \begin{aligned}U(r_2)-U(r_1)&=\int^{r_2}_{r_1}{dU}\\&=\dfrac{G m_1m_2}{r^2} dr\\&=G m_1m_2\int^{r_2}_{r_1}\dfrac{1}{r^2}\\&=-Gm_1m_2\left[\dfrac{1}{r}\right]^{r_2}_{r_1}\\&=-Gm_1m_2\left[\dfrac{1}{r_2}-\dfrac{1}{r_1}\right]\\&=Gm_1m_2\left[\dfrac{1}{r_1}-\dfrac{1}{r_2}\right]\end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8a6a1a273eec33468334cadde7f8bedb_l3.png)
Expression for Gravitational Potential Energy at Height (h)
When an object is taken off from the Earth’s surface to a point ‘h’ above the Earth’s surface and the mass of the Earth is taken to be M and the mass of the object is m, such that,
r1 = R
r2 = R +h
Then,
ΔU = GMm/R – GMm/(R+h)
ΔU = GMm [1/R – 1/(R+h)]
ΔU = GMmh/R(R + h)
For a very small value of h R + h >>> h such that, R +h = r and g = GM/R2
On Substituting, we get
ΔU = mgh
What is Gravitational Potential?
Gravitational Potential is defined as the amount of work done in moving a unit test mass from infinity into the gravitational field of the source mass.
Gravitational Potential Energy possessed by the unit test mass is called Gravitational Potential. It is represented by the symbol V.
V = U/m
V = -GM/r
Gravitational potential at a point is always negative and is maximum at infinity.
Relation between Gravitational Field Intensity and Gravitational Potential
The integral form of the gravitational field is,
V = – 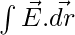
where,
V is Gravitational Potential
E is Gravitational Field Intensity
Differential form of Gravitational Field Intensity and Gravitational Potential is,
E = -dV/dr
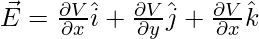
Gravitational Potential of Point Mass
For a point mass of mass M, the gravitational potential at a distance ‘r’ from the point mass is given by the formula,
V = – GM/r
Gravitational Potential of a Spherical Shell
The Gravitational Potential of a Spherical Shell is calculated using the Gravitational Potential formula,
Now for calculating the Gravitational Potential of a Spherical Shell consider a thin uniform spherical shell of the radius (R) and mass (M), then
Case 1: At point ‘P’ which is inside the spherical shell such that r<R.
V is a constant as E = 0 and the gravitational potential is given by,
V = -GM/R
Case 2: At point ‘P’ which is at the surface of the spherical shell such that r = R.
we know that, E = -GM/R2.
Now,
V = – 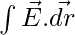
solving the integral from (0 to R), we get, Gravitational Potential as
V = -GM/R
Case 3: At point ‘P’ which is outside the spherical shell such that r>R
We know that E = -GM/r2.
Now,
V = – 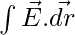
solving the integral from (0 to r), we get, Gravitational Potential as
V = -GM/r
Gravitational Potential of a Uniform Solid Sphere
The Gravitational Potential of a uniform solid sphere can easily be calculated using the gravitational potential formula. Let’s consider a thin uniform solid sphere of the radius (R) and mass (M) then,
Case 1: At point ‘P’ which is inside the solid sphere such that r<R, the gravitational potential is given by,
E = -GMr/R3
Now,
V = – 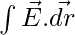
Integrating over the limit from (0 to r)
Now the Gravitational Potential is given by,
V = -GM [(3R2 – r2)/2R2]
Case 2: At point ‘P’ at the surface of the solid sphere such that r = R
E = -GM/R2
V = – 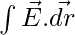
Integrating over the limit from (0 to r)
V = -GM/R
Case 3: At point ‘P’ outside the solid sphere such that r > R
V = -GM/R
Case 4: At the centre of the solid sphere gravitational potential is given by,
V =(-3/2) × (GM/R)
Gravitational Self Energy
The work done by an external agent in collecting the infinitesimal elements of a body that are initially at an infinite distance from each other is defined as Gravitational Self Energy
Gravitational Self-Energy of the system of ‘n’ Particles
Gravitational Self-Energy of the system of ‘n’ particles is calculated as Let’s consider n particle system where particles interact with each other and their average distance is ‘r’. They interact with each other mutually due to their gravitational force.
The total interactions between them are n(n – 1)/2 and the potential energy of the system is equal to the sum of the potential energy of all the pairs of particles, which is calculated as,
Us = 1/2 × [Gn(n-1)m2] / r2
What is the mass of the Earth?
The mass of the earth can easily be calculated using the Universal Gravitational Constant and gravity of the earth.
We know acceleration due to gravity at the surface of the earth is given by,
g = (G× M) / R2 …(1)
where
G is the Universal Gravitational Constant
R is the radius of the earth
g is the acceleration due to gravity
M is the mass of earth
We know that,
- G = 6.67 × 10-11 Nm2kg-2
- R = 6.38 × 106 m
- g = 9.8 m/s2
M =?
To calculate M substitute the above value in eq (1)
9.8 = (6.67 × 10-11 × M) / (6.38 × 106)2,
M = (9.8 × (6.38× 106)2) / (6.67 ×10-11)
M = 5.98 × 1024 kg
Thus, the mass of the Earth is 5.98 × 1024 kg
Read, More
Solved Examples on Gravitational Potential Energy
Example 1: The Gravitational field intensity at a point 5 × 104 km from the surface of the earth is 4 N/kg. Calculate the gravitational potential at that point.
Solution:
Gravitational field intensity is given by,
E = F / m
4 N/kg = (G × M × m) / (r2 × m)
= (G × M) / r2, where r is the distance between the centre of the earth and the body.
i.e. r = R + 5×104 km, R is the radius of the Earth, R = 6.4 × 106 m.
r = 6.4 × 106 + 5 × 107 m
= 5.64 × 107 m
Therefore,
4 N/kg = (G × M) / (5.64 × 107)2
4 N/kg × (5.64 × 107)2 = G × M
Gravitational Potential (V) = -(G × M) / r
= – (4 × (5.64 × 107)2 ) / (5.64 × 107) J/kg
V = – 2.256 × 108 J/kg.
Example 2: Derive an expression for the amount of work done to move a body from the Earth’s surface to infinity i.e. beyond Earth’s gravitational field.
Solution:
We know Work done (W) = Force × displacement.
But we cannot use this formula directly because gravitational force is not constant. This formula works when force remains constant throughout the motion.
Therefore we will use integration as,
dW = F × dr
dW = (G × M × m / r2) × dr
Integrating W from R to infinity because the body is being moved from the earth’s surface to infinity.
W = R∫∞ ((G × M × m) / r2 ) × dr
W = (GMm) / R
Example 3: Discuss the variation of acceleration due to gravity with altitude and depth.
Solution:
Acceleration due to gravity is maximum at the surface of the earth. It decreases with the increase in altitude and depth.
Variation of g with altitude:
g’ = g – [(2 h g) / R]—(1)
Considering equation (1), it is clear that with the increase in height t(h) value of g’ decreases because 2, g and R are constants.
g’ is the acceleration due to gravity at a height h from the surface of the earth, g is the acceleration due to gravity at the surface of the earth, g = 9.8 m/s2, and R is the radius of the earth,
R = 6.38 × 106 m
Variation of g with depth:
g’ = g [1 -(d/R)]—(2)
Considering equation (2), it is clear that with the increase in depth(d) value of g’ decreases because g and R are constants.
g’ is the acceleration due to gravity at a depth d from the surface of the earth, g is a constant i.e. it is the acceleration due to gravity at the surface of the earth, g = 9.8 m/s2 and R is the radius of the earth.
Hence the acceleration due to gravity is maximum at the surface of the earth.
Example 4: A 10 kg block free falls from rest from a height of 20 m. Determine the work done by the force of gravity and the change in gravitational potential energy. Consider the acceleration due to gravity to be 10 m/s2.
Solution:
We know that,
The work done by the force of gravity, W = mgh
where m is mass, g is the gravitational acceleration and h is the height.
Substituting the values in the above equation, we get
W = 10 kg × 20 m × 10 m/s2
= 200 N
The change in gravitational potential energy is equal to the work done by gravity.
Therefore, Gravitational Potential Energy is also equal to 200 Joule.
FAQs on Gravitational Potential Energy
Question 1: What is Gravitational Potential?
Answer:
When a body of unit mass is displaced from infinity to a point inside the gravitational field the work done in moving that particle is referred to as Gravitational Potential which is denoted by V.
Question 2: What is the expression for gravitational potential energy?
Answer:
Gravitational Potential Energy can be calculated using,
V = -GMm/r
where,
M is the source mass placed along the x-axis
m is the test mass at infinity
r is the distance between the source mass and the test mass
Question 3: What is the Unit of Gravitational Potential?
Answer:
The Unit of Gravitational Potential is J/kg.
Question 4: What is the Dimensional formula of Gravitational Potential?
Answer:
The Dimensional formula of Gravitational Potential is [M0L2T-2].
Question 5: Is Gravitational Potential a Vector Quantity?
Answer:
No, Gravitational potential is not a vector quantity it is a scalar quantity.
Question 6: What is the maximum value of gravitational potential energy?
Answer:
The value of Gravitational potential is maximum at infinity.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...