Graphical Representation of Data: In today’s world of the internet and connectivity, there is a lot of data available, and some or other method is needed for looking at large data, the patterns, and trends in it. There is an entire branch in mathematics dedicated to dealing with collecting, analyzing, interpreting, and presenting numerical data in visual form in such a way that it becomes easy to understand and the data becomes easy to compare as well, the branch is known as Statistics.
The branch is widely spread and has a plethora of real-life applications such as Business Analytics, demography, Astro statistics, and so on. In this article, we have provided everything about the graphical representation of data, including its types, rules, advantages, etc.
What is Graphical Representation
Graphics Representation is a way of representing any data in picturized form. It helps a reader to understand the large set of data very easily as it gives us various data patterns in visualized form.
There are two ways of representing data,
- Tables
- Pictorial Representation through graphs.
They say, “A picture is worth a thousand words”. It’s always better to represent data in a graphical format. Even in Practical Evidence and Surveys, scientists have found that the restoration and understanding of any information is better when it is available in the form of visuals as Human beings process data better in visual form than any other form.
Does it increase the ability 2 times or 3 times? The answer is it increases the Power of understanding 60,000 times for a normal Human being, the fact is amusing and true at the same time.
Types of Graphical Representations
Comparison between different items is best shown with graphs, it becomes easier to compare the crux of the data about different items. Let’s look at all the different types of graphical representations briefly:
Line Graphs
A line graph is used to show how the value of a particular variable changes with time. We plot this graph by connecting the points at different values of the variable. It can be useful for analyzing the trends in the data and predicting further trends.
Bar Graphs
A bar graph is a type of graphical representation of the data in which bars of uniform width are drawn with equal spacing between them on one axis (x-axis usually), depicting the variable. The values of the variables are represented by the height of the bars.
Histograms
This is similar to bar graphs, but it is based frequency of numerical values rather than their actual values. The data is organized into intervals and the bars represent the frequency of the values in that range. That is, it counts how many values of the data lie in a particular range.
Line Plot
It is a plot that displays data as points and checkmarks above a number line, showing the frequency of the point.
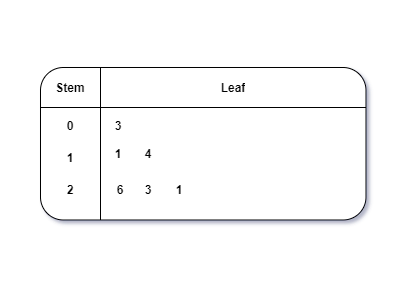
Stem and Leaf Plot
This is a type of plot in which each value is split into a “leaf”(in most cases, it is the last digit) and “stem”(the other remaining digits). For example: the number 42 is split into leaf (2) and stem (4).
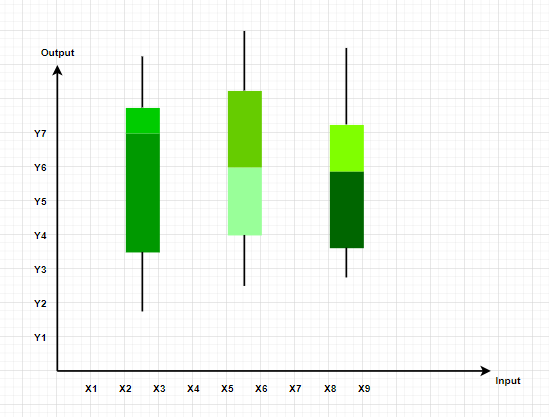
Box and Whisker Plot
These plots divide the data into four parts to show their summary. They are more concerned about the spread, average, and median of the data.
Pie Chart
It is a type of graph which represents the data in form of a circular graph. The circle is divided such that each portion represents a proportion of the whole.

Graphical Representations used in Maths
Graphs in Math are used to study the relationships between two or more variables that are changing. Statistical data can be summarized in a better way using graphs. There are basically two lines of thoughts of making graphs in maths:
- Value-Based or Time Series Graphs
- Frequency Based
Value-Based or Time Series Graphs
These graphs allow us to study the change of a variable with respect to another variable within a given interval of time. The variables can be anything. Time Series graphs study the change of variable with time. They study the trends, periodic behavior, and patterns in the series. We are more concerned with the values of the variables here rather than the frequency of those values.
Example: Line Graph
Frequency Based
These kinds of graphs are more concerned with the distribution of data. How many values lie between a particular range of the variables, and which range has the maximum frequency of the values. They are used to judge a spread and average and sometimes median of a variable under study.
Example: Frequency Polygon, Histograms.
Principles of Graphical Representations
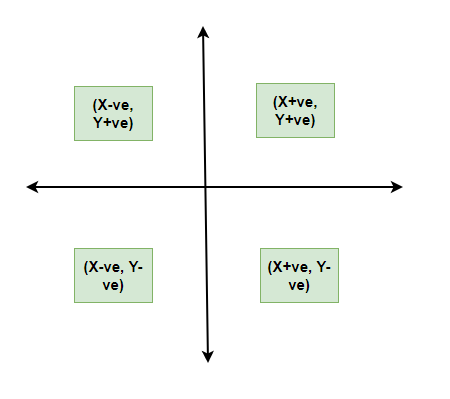
All types of graphical representations require some rule/principles which are to be followed. These are some algebraic principles. When we plot a graph, there is an origin, and we have our two axes. These two axes divide the plane into four parts called quadrants. The horizontal one is usually called the x-axis and the other one is called the y-axis. The origin is the point where these two axes intersect.
The thing we need to keep in mind about the values of the variable on the x-axis is that positive values need to be on the right side of the origin and negative values should be on the left side of the origin. Similarly, for the variable on the y-axis, we need to make sure that the positive values of this variable should be above the x-axis and negative values of this variable must be below the y-axis.
Advantages and Disadvantages of Using Graphical System
Advantages
- It gives us a summary of the data which is easier to look at and analyze.
- It saves time.
- We can compare and study more than one variable at a time.
Disadvantages
It usually takes only one aspect of the data and ignores the other. For example, A bar graph does not represent the mean, median, and other statistics of the data.
General Rules for Graphical Representation of Data
We should keep in mind some things while plotting and designing these graphs. The goal should be a better and clear picture of the data. Following things should be kept in mind while plotting the above graphs:
- Whenever possible, the data source must be mentioned for the viewer.
- Always choose the proper colors and font sizes. They should be chosen to keep in mind that the graphs should look neat.
- The measurement Unit should be mentioned in the top right corner of the graph.
- The proper scale should be chosen while making the graph, it should be chosen such that the graph looks accurate.
- Last but not the least, a suitable title should be chosen.
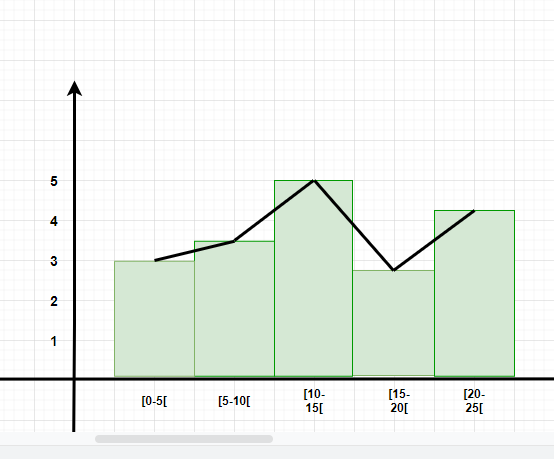
Frequency Polygon
A frequency polygon is a graph that is constructed by joining the midpoint of the intervals. The height of the interval or the bin represents the frequency of the values that lie in that interval.
Must Read
Solved Examples on Graphical Representation of Data
Question 1: What are different types of frequency-based plots?
Answer:
Types of frequency based plots:
- Histogram
- Frequency Polygon
- Box Plots
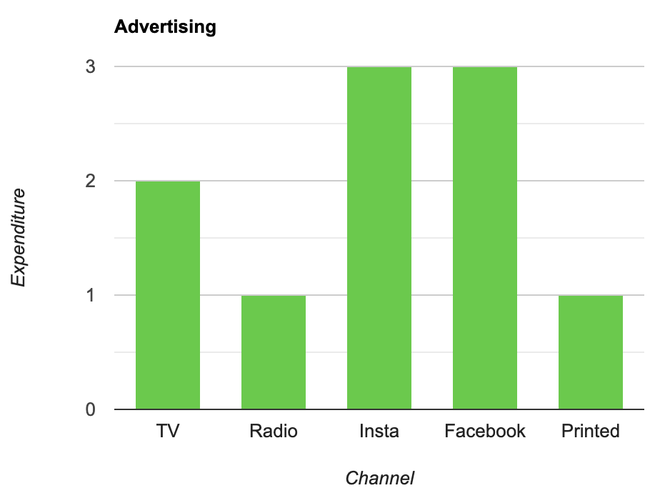
Question 2: A company with an advertising budget of Rs 10,00,00,000 has planned the following expenditure in the different advertising channels such as TV Advertisement, Radio, Facebook, Instagram, and Printed media. The table represents the money spent on different channels.
| Advertising Channel |
Expenditure (In Crores) |
| TV Advertisement |
2 |
| Radio |
1 |
| Facebook |
3 |
| Instagram |
3 |
| Printed Media |
1 |
Draw a bar graph for the following data.
Solution:
Steps:
- Put each of the channels on the x-axis
- The height of the bars is decided by the value of each channel.
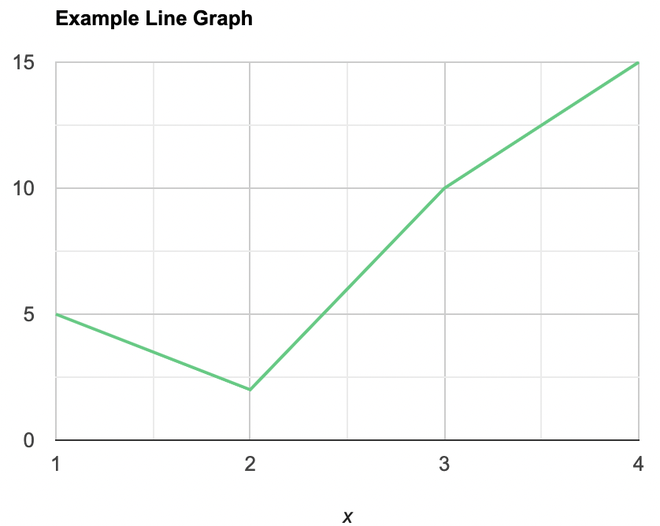
Question 3: Draw a line plot for the following data
| x |
1 |
2 |
3 |
4 |
5 |
6 |
| y |
5 |
2 |
10 |
15 |
12 |
8 |
Solution:
Steps:
- Put each of the x-axis row value on the x-axis
- joint the value corresponding to the each value of the x-axis.
Question 4: Make a frequency plot of the following data:
| x |
[0-3] |
[3-16] |
[6-9] |
[9-12] |
| y |
3 |
4 |
2 |
6 |
Solution:
Steps:
- Draw the class intervals on the x-axis and frequencies on the y-axis.
- Calculate the mid point of each class interval.
| Class Interval |
Mid Point |
Frequency |
| 0-3 |
1.5 |
3 |
| 3-6 |
4.5 |
4 |
| 6-9 |
7.5 |
2 |
| 9-12 |
10.5 |
6 |
Now join the mid points of the intervals and their corresponding frequencies on the graph.
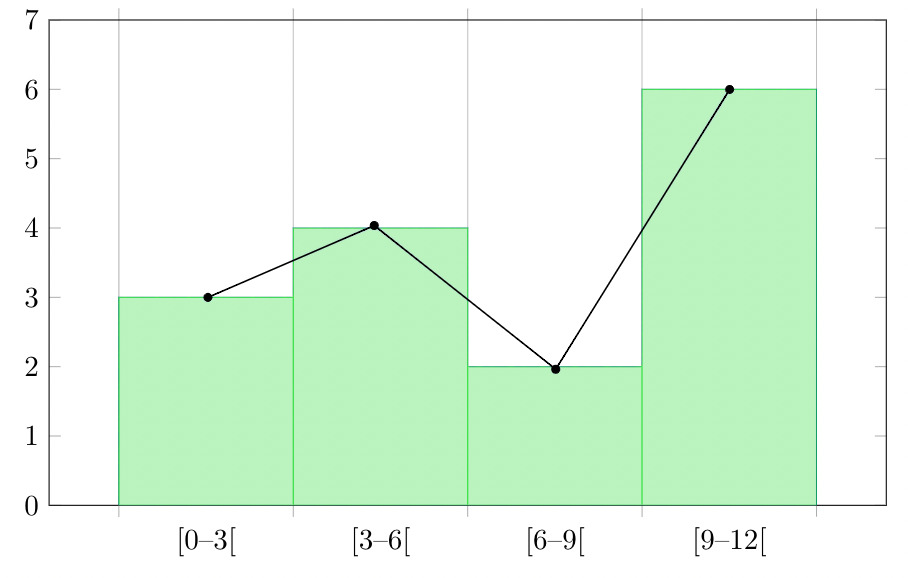
This graph shows both the histogram and frequency polygon for the given distribution.
Graphical Representation of Data – FAQs
What are the advantages of using graphs to represent data?
Graphs offer visualization, clarity, and easy comparison of data, aiding in outlier identification and predictive analysis.
What are the common types of graphs used for data representation?
Common graph types include bar, line, pie, histogram, and scatter plots, each suited for different data representations and analysis purposes.
How do you choose the most appropriate type of graph for your data?
Select a graph type based on data type, analysis objective, and audience familiarity to effectively convey information and insights.
How do you create effective labels and titles for graphs?
Use descriptive titles, clear axis labels with units, and legends to ensure the graph communicates information clearly and concisely.
How do you interpret graphs to extract meaningful insights from data?
Interpret graphs by examining trends, identifying outliers, comparing data across categories, and considering the broader context to draw meaningful insights and conclusions.
Share your thoughts in the comments
Please Login to comment...