Types of Graphs with Examples
Last Updated :
05 May, 2023
A Graph is a non-linear data structure consisting of nodes and edges. The nodes are sometimes also referred to as vertices and the edges are lines or arcs that connect any two nodes in the graph. More formally a Graph can be defined as, A Graph consisting of a finite set of vertices(or nodes) and a set of edges that connect a pair of nodes
- Undirected Graphs: A graph in which edges have no direction, i.e., the edges do not have arrows indicating the direction of traversal. Example: A social network graph where friendships are not directional.
- Directed Graphs: A graph in which edges have a direction, i.e., the edges have arrows indicating the direction of traversal. Example: A web page graph where links between pages are directional.
- Weighted Graphs: A graph in which edges have weights or costs associated with them. Example: A road network graph where the weights can represent the distance between two cities.
- Unweighted Graphs: A graph in which edges have no weights or costs associated with them. Example: A social network graph where the edges represent friendships.
- Complete Graphs: A graph in which each vertex is connected to every other vertex. Example: A tournament graph where every player plays against every other player.
- Bipartite Graphs: A graph in which the vertices can be divided into two disjoint sets such that every edge connects a vertex in one set to a vertex in the other set. Example: A job applicant graph where the vertices can be divided into job applicants and job openings.
- Trees: A connected graph with no cycles. Example: A family tree where each person is connected to their parents.
- Cycles: A graph with at least one cycle. Example: A bike-sharing graph where the cycles represent the routes that the bikes take.
- Sparse Graphs: A graph with relatively few edges compared to the number of vertices. Example: A chemical reaction graph where each vertex represents a chemical compound and each edge represents a reaction between two compounds.
- Dense Graphs: A graph with many edges compared to the number of vertices. Example: A social network graph where each vertex represents a person and each edge represents a friendship.
Types of Graphs:
1. Finite Graphs
A graph is said to be finite if it has a finite number of vertices and a finite number of edges. A finite graph is a graph with a finite number of vertices and edges. In other words, both the number of vertices and the number of edges in a finite graph are limited and can be counted. Finite graphs are often used to model real-world situations, where there is a limited number of objects and relationships between the
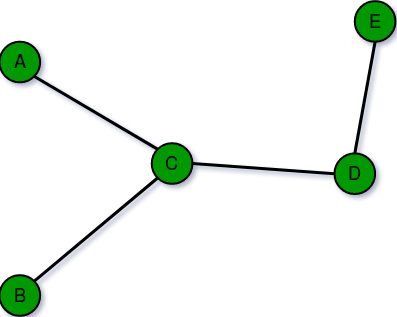
2. Infinite Graph:
A graph is said to be infinite if it has an infinite number of vertices as well as an infinite number of edges.
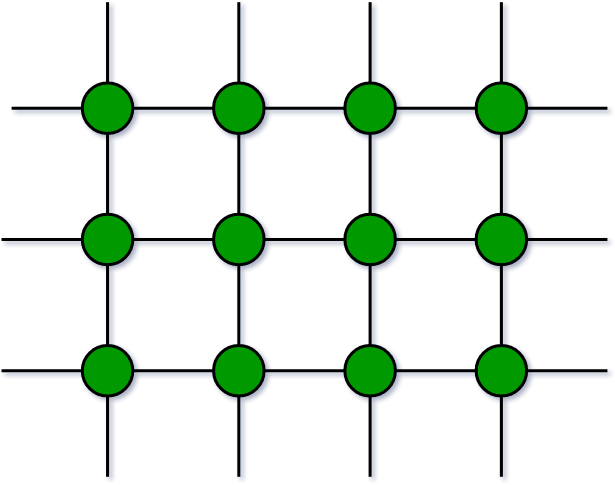
3. Trivial Graph:
A graph is said to be trivial if a finite graph contains only one vertex and no edge. A trivial graph is a graph with only one vertex and no edges. It is also known as a singleton graph or a single vertex graph. A trivial graph is the simplest type of graph and is often used as a starting point for building more complex graphs. In graph theory, trivial graphs are considered to be a degenerate case and are not typically studied in detail
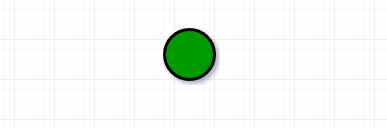
4. Simple Graph:
A simple graph is a graph that does not contain more than one edge between the pair of vertices. A simple railway track connecting different cities is an example of a simple graph.

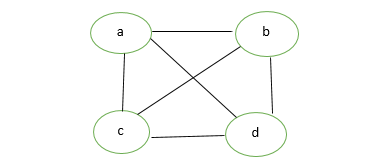
5. Multi Graph:
Any graph which contains some parallel edges but doesn’t contain any self-loop is called a multigraph. For example a Road Map.
- Parallel Edges: If two vertices are connected with more than one edge then such edges are called parallel edges that are many routes but one destination.
- Loop: An edge of a graph that starts from a vertex and ends at the same vertex is called a loop or a self-loop.
6. Null Graph:
A graph of order n and size zero is a graph where there are only isolated vertices with no edges connecting any pair of vertices.A null graph is a graph with no edges. In other words, it is a graph with only vertices and no connections between them. A null graph can also be referred to as an edgeless graph, an isolated graph, or a discrete graph
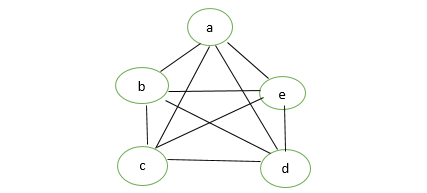
7. Complete Graph:
A simple graph with n vertices is called a complete graph if the degree of each vertex is n-1, that is, one vertex is attached with n-1 edges or the rest of the vertices in the graph. A complete graph is also called Full Graph.

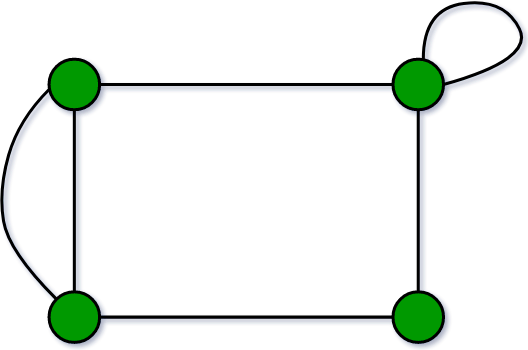
8. Pseudo Graph:
A graph G with a self-loop and some multiple edges is called a pseudo graph. A pseudograph is a type of graph that allows for the existence of loops (edges that connect a vertex to itself) and multiple edges (more than one edge connecting two vertices). In contrast, a simple graph is a graph that does not allow for loops or multiple edges.
9. Regular Graph:
A simple graph is said to be regular if all vertices of graph G are of equal degree. All complete graphs are regular but vice versa is not possible. A regular graph is a type of undirected graph where every vertex has the same number of edges or neighbors. In other words, if a graph is regular, then every vertex has the same degree.
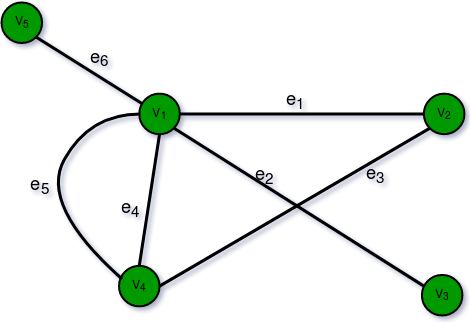
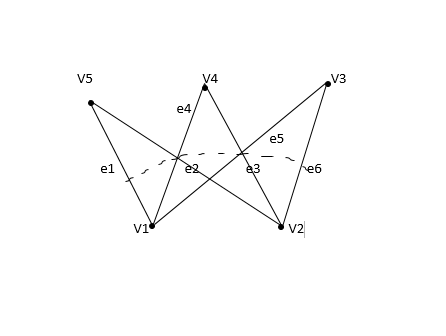
10. Bipartite Graph:
A graph G = (V, E) is said to be a bipartite graph if its vertex set V(G) can be partitioned into two non-empty disjoint subsets. V1(G) and V2(G) in such a way that each edge e of E(G) has one end in V1(G) and another end in V2(G). The partition V1 U V2 = V is called Bipartite of G. Here in the figure: V1(G)={V5, V4, V3} and V2(G)={V1, V2}
11. Labeled Graph:
If the vertices and edges of a graph are labeled with name, date, or weight then it is called a labeled graph. It is also called Weighted Graph.
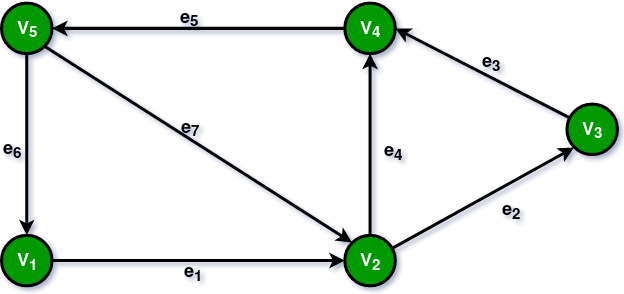
12. Digraph Graph:
A graph G = (V, E) with a mapping f such that every edge maps onto some ordered pair of vertices (Vi, Vj) are called a Digraph. It is also called Directed Graph. The ordered pair (Vi, Vj) means an edge between Vi and Vj with an arrow directed from Vi to Vj. Here in the figure: e1 = (V1, V2) e2 = (V2, V3) e4 = (V2, V4)
13. Subgraph:
A graph G1 = (V1, E1) is called a subgraph of a graph G(V, E) if V1(G) is a subset of V(G) and E1(G) is a subset of E(G) such that each edge of G1 has same end vertices as in G.

14. Connected or Disconnected Graph:
Graph G is said to be connected if any pair of vertices (Vi, Vj) of a graph G is reachable from one another. Or a graph is said to be connected if there exists at least one path between each and every pair of vertices in graph G, otherwise, it is disconnected. A null graph with n vertices is a disconnected graph consisting of n components. Each component consists of one vertex and no edge.
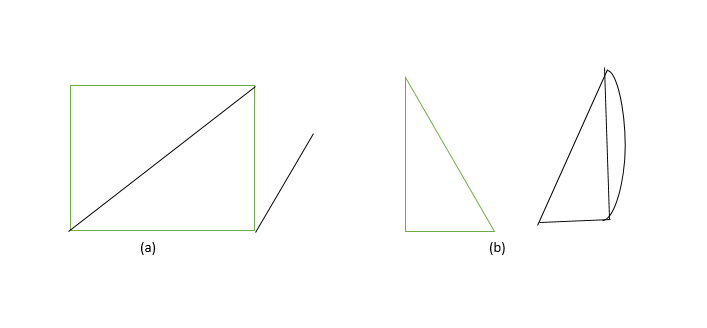
15. Cyclic Graph:
A graph G consisting of n vertices and n> = 3 that is V1, V2, V3- – – – Vn and edges (V1, V2), (V2, V3), (V3, V4)- – – – (Vn, V1) are called cyclic graph.
16. Types of Subgraphs:
- Vertex disjoint subgraph: Any two graph G1 = (V1, E1) and G2 = (V2, E2) are said to be vertex disjoint of a graph G = (V, E) if V1(G1) intersection V2(G2) = null. In the figure, there is no common vertex between G1 and G2.
- Edge disjoint subgraph: A subgraph is said to be edge-disjoint if E1(G1) intersection E2(G2) = null. In the figure, there is no common edge between G1 and G2.
Note: Edge disjoint subgraph may have vertices in common but a vertex disjoint graph cannot have a common edge, so the vertex disjoint subgraph will always be an edge-disjoint subgraph.
17. Spanning Subgraph
Consider the graph G(V,E) as shown below. A spanning subgraph is a subgraph that contains all the vertices of the original graph G that is G'(V’,E’) is spanning if V’=V and E’ is a subset of E.
So one of the spanning subgraph can be as shown below G'(V’,E’). It has all the vertices of the original graph G and some of the edges of G.
This is just one of the many spanning subgraphs of graph G. We can create various other spanning subgraphs by different combinations of edges. Note that if we consider a graph G'(V’,E’) where V’=V and E’=E, then graph G’ is a spanning subgraph of graph G(V,E).
Advantages of graphs:
- Graphs can be used to model and analyze complex systems and relationships.
- They are useful for visualizing and understanding data.
- Graph algorithms are widely used in computer science and other fields, such as social network analysis, logistics, and transportation.
- Graphs can be used to represent a wide range of data types, including social networks, road networks, and the internet.
Disadvantages of graphs:
- Large graphs can be difficult to visualize and analyze.
- Graph algorithms can be computationally expensive, especially for large graphs.
- The interpretation of graph results can be subjective and may require domain-specific knowledge.
- Graphs can be susceptible to noise and outliers, which can impact the accuracy of analysis results.
Related article: Applications, Advantages and Disadvantages of Graph
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...