Graph measurements: length, distance, diameter, eccentricity, radius, center
Last Updated :
31 Oct, 2022
Prerequisite – Graph Theory Basics – Set 1, Set 2
A graph is defined as set of points known as ‘Vertices’ and line joining these points is known as ‘Edges’. It is a set consisting of where ‘V’ is vertices and ‘E’ is edge.
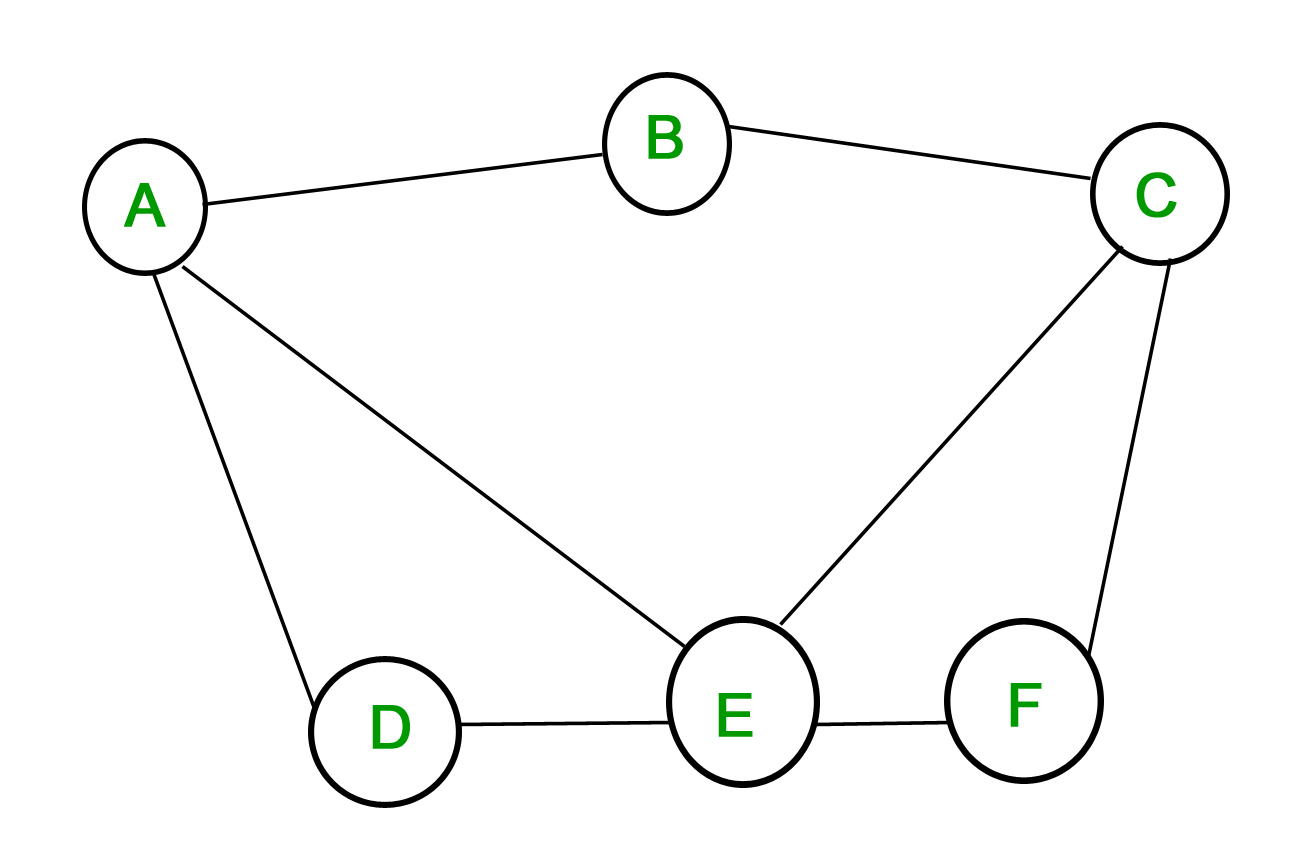
Vertices: {A, B, C, D, E, F}
Edges: {{A, B}, {A, D}, {A, E}, {B, C}, {C, E}, {C, F}, {D, E}, {E, F}}
Graph Measurements: There are few graph measurement methods available:
1. Length –
Length of the graph is defined as the number of edges contained in the graph.
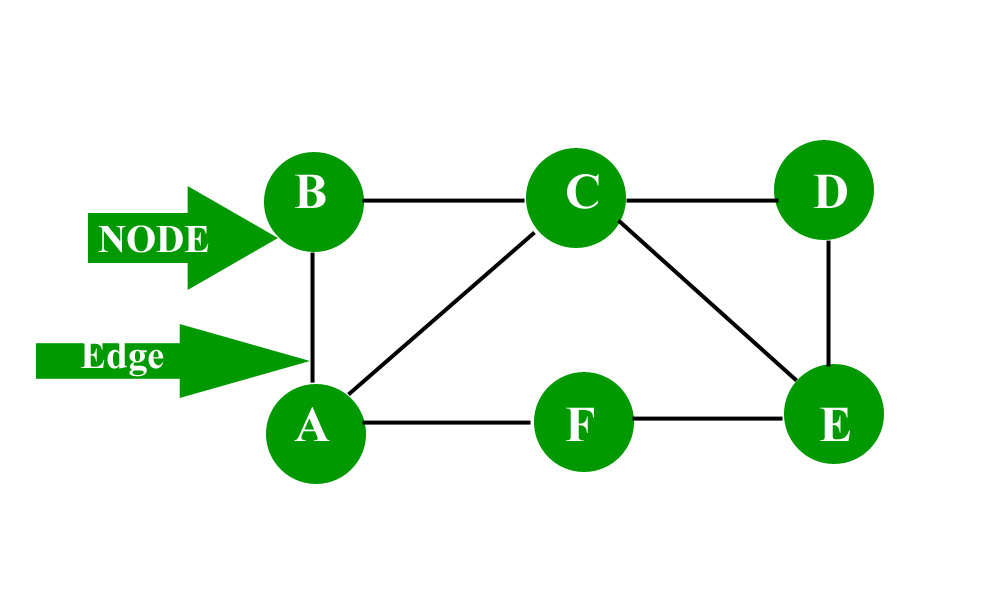
Length of the graph: 8
AB, BC, CD, DE, EF, FA, AC, CE
2. The distance between two Vertices –
The distance between two vertices in a graph is the number of edges in a shortest or minimal path. It gives the available minimum distance between two edges. There can exist more than one shortest path between two vertices.

Shortest Distance between 1 – 5 is 2
1 → 2 → 5
3. Eccentricity of graph –
It is defined as the maximum distance of one vertex from other vertex. The maximum distance between a vertex to all other vertices is considered as the eccentricity of the vertex. It is denoted by e(V).

Eccentricity from:
(A, A) = 0
(A, B) = 1
(A, C) = 2
(A, D) = 1
Maximum value is 2, So Eccentricity is 2
4. Diameter of graph –
The diameter of graph is the maximum distance between the pair of vertices. It can also be defined as the maximal distance between the pair of vertices. Way to solve it is to find all the paths and then find the maximum of all. It can also be found by finding the maximum value of eccentricity from all the vertices.

Diameter: 3
BC → CF → FG
Here the eccentricity of the vertex B is 3 since (B,G) = 3. (Maximum Eccentricity of Graph)
5. Radius of graph –A radius of the graph exists only if it has the diameter. The minimum among all the maximum distances between a vertex to all other vertices is considered as the radius of the Graph G. It is denoted as r(G). It can also be found by finding the minimum value of eccentricity from all the vertices.

Radius: 2
All available minimum radius:
BC → CF,
BC → CE,
BC → CD,
BC → CA
6. Centre of graph –
It consists of all the vertices whose eccentricity is minimum. Here the eccentricity is equal to the radius. For example, if the school is at the center of town it will reduce the distance buses has to travel. If eccentricity of two vertex is same and minimum among all other both of them can be the center of the graph.

Centre: A
Inorder to find the center of the graph, we need to find the eccentricity of each vertex and find the minimum among all of them.
The minimum eccentricity vertex will be considered as the center.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...