Given two arrays, find n+m-1 unique sum pairs

Given 2 integer arrays A and B(with no repeated elements in each) of size N and M respectively, form N + M – 1 pairs, each pair having one element from both the arrays, such that the sum of all the pairs is unique. For each pair, print the index of the elements in their respective array. Example:

Input: N = 5, M = 3
       A = [6, 5, 7, 1, 3]
       B = [2, 4, 8]

Output: 2 0
        2 1
        2 2
        3 0
        4 0
        1 0
        0 0

We have to form 5 + 3 - 1 = 7 pairs. These pairs are:
(7, 2), (7, 4), (7, 8), (1, 2), (3, 2), (5, 2), (6, 2)
All have unique sum

Brute Force Approach: We can run a loop on both arrays A and B to find the first N+M-1 unique sum pairs, and print their indexes along the way. To check if a particular sum has already been used, we make a python bool dictionary. If the dictionary value for that sum is False, that means it is a new sum value. If it is True, the sum has already been used.

Code:

from collections import defaultdict as dd

# Function to form unique sum pairs
def unique_pairs():

    # Python Bool Dictionary
    d = dd(bool)
    ct = 0

    # For every element of A, Find
    # a unique sum pair in B. Break
    # the loop after N + M-1 pairs
    for i in range(n):
        for j in range(m):
            if(ct == n + m-1):
                break
            sm = a[i] + b[j]
            if(d[sm] == False):
                d[sm] = True
                ct+= 1
                print(i, j)

n, m = 6, 4
a = [ 6, 4, 3, 5, 8, 2 ]
b = [ 3, 5, 4, 2 ]

unique_pairs()

Output:

0 0
0 1
0 2
0 3
1 0
1 3
2 3
4 1
4 2

Time Complexity: Since we traverse the array with nested loops, the time complexity comes out to be O().
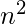
Efficient Approach: Once we sort both the arrays, first we can make N unique sum pairs by pairing all elements of array A with the first element of array B, and then pairing the other M – 1 elements of array B with the last element of array A. Code:

from collections import defaultdict as dd

# Function to form unique sum pairs
def unique_pairs_sort():

    # Python Int Dictionary
    da = dd(int)
    db = dd(int)

    # Make a dictionary to store index
    for i in range(n):
        da[a[i]] = i
    for i in range(m):
        db[b[i]] = i

    # Sorting the arrays
    a.sort(); b.sort()

    # N pairs of A with B[0]
    for i in range(n):
        print(da[a[i]], db[b[0]])

    # M-1 pairs of B with A[N-1]
    for i in range(1, m):
        print(da[a[-1]], db[b[i]])

n, m = 6, 4
a = [ 6, 4, 3, 5, 8, 2 ]
b = [ 3, 5, 4, 2 ]

unique_pairs_sort()

Output:

5 3
2 3
1 3
3 3
0 3
4 3
4 0
4 2
4 1

Time Complexity: The complexity for this is equal to the time required for sorting: O(n Log n). Space Complexity: Since we are using two different maps/dictionaries to store the indexes of the array. The time complexity will be O(n + m) , where n is the size of first array and m is the size of second array.