Gill’s 4th Order Method to solve Differential Equations

Last Updated : 15 Nov, 2021

Given the following inputs:

An ordinary differential equation that defines the value of dy/dx in the form x and y.
$\LARGE \frac{dy}{dx} = f(x, y)$
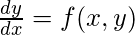
Initial value of y, i.e., y(0).
$\LARGE y(0)= y_o$

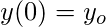
The task is to find the value of the unknown function y at a given point x, i.e. y(x).
Examples:

Input: x0 = 0, y = 3.0, x = 5.0, h = 0.2
Output: y(x) = 3.410426
Input: x0 = 0, y = 1, x = 3, h = 0.3
Output: y(x) = 1.669395

Approach:
Gill’s method is used to find an approximate value of y for a given x. Below is the formula used to compute the next value y_n+1 from the previous value y_n.
Therefore:

y_n+1 = value of y at (x = n + 1)
y_n = value of y at (x = n)
where
  0 ? n ? (x - x₀)/h
  h is step height
  x_n+1 = x₀ + h

The essential formula to compute the value of y(n+1):
$\LARGE K_{1} = h*f(x_{n}, y_{n})$
$\LARGE K_{2} = h*f(x_n + \frac{1}{2}h, y_n + \frac{1}{2}k_1)$
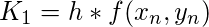
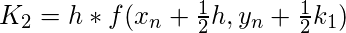
$\LARGE K_{3} = h*f[x_n + \frac{1}{2}h, y_n + \frac{1}{2}(-1 + \sqrt{2})k_1 + (1 - \frac{1}{2}\sqrt{2})k_2]$
$\LARGE K_{4} = h*f[x_n + h, y_n - \frac{1}{2}\sqrt{2}k_2 + (1 + \frac{1}{2}\sqrt{2})k_3]$
$\LARGE y_{n+1} = y_{n} + \frac{1}/{6}[K_1 + (2 - \sqrt{2})K_{2} + (2 + \sqrt{2})K_3 + K_4 ] + Error Terms$
The formula basically computes the next value y_n+1 using current y_n:

K₁ is the increment based on the slope at the beginning of the interval, using y.
K₂ is the increment based on the slope, using
$\LARGE (y + \frac{1}{2}(K_1*h))$
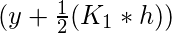
K₃ is the increment based on the slope, using
$\LARGE (y + \frac{1}{2}(-1 + \sqrt{2})K_1 + (1 - \frac{1}{2}\sqrt{2})K_2)$
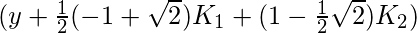
K₄ is the increment based on the slope, using
$(y - \frac{1}{2}\sqrt{2}K_2 + (1 + \frac{1}{2}\sqrt{2})K_3)$

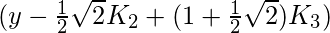
The method is a fourth-order method, meaning that the local truncation error is of the order of O(h⁵).
Below is the implementation of the above approach:

C++

// C++ program to implement Gill's method
 
#include <bits/stdc++.h>
using namespace std;
 
// A sample differential equation
// "dy/dx = (x - y)/2"
float dydx(float x, float y)
{
    return (x - y) / 2;
}
 
// Finds value of y for a given x
// using step size h and initial
// value y0 at x0
float Gill(float x0, float y0,
        float x, float h)
{
    // Count number of iterations
    // using step size or height h
    int n = (int)((x - x0) / h);
 
    // Value of K_i
    float k1, k2, k3, k4;
 
    // Initial value of y(0)
    float y = y0;
 
    // Iterate for number of iteration
    for (int i = 1; i <= n; i++) {
 
        // Apply Gill's Formulas to
        // find next value of y
 
        // Value of K1
        k1 = h * dydx(x0, y);
 
        // Value of K2
        k2 = h * dydx(x0 + 0.5 * h,
                    y + 0.5 * k1);
 
        // Value of K3
        k3 = h * dydx(x0 + 0.5 * h,
                    y + 0.5 * (-1 + sqrt(2)) * k1
                        + k2 * (1 - 0.5 * sqrt(2)));
 
        // Value of K4
        k4 = h * dydx(x0 + h,
                    y - (0.5 * sqrt(2)) * k2
                        + k3 * (1 + 0.5 * sqrt(2)));
 
        // Find the next value of y(n+1)
        // using y(n) and values of K in
        // the above steps
        y = y + (1.0 / 6) * (k1 + (2 - sqrt(2)) * k2 
                            + (2 + sqrt(2)) * k3 + k4);
 
        // Update next value of x
        x0 = x0 + h;
    }
 
    // Return the final value of dy/dx
    return y;
}
 
// Driver Code
int main()
{
    float x0 = 0, y = 3.0,
        x = 5.0, h = 0.2;
 
    printf("y(x) = %.6f",
        Gill(x0, y, x, h));
    return 0;
}

Java

// Java program to implement Gill's method
class GFG{
 
// A sample differential equation
// "dy/dx = (x - y)/2"
static double dydx(double x, double y)
{
    return (x - y) / 2;
}
 
// Finds value of y for a given x
// using step size h and initial
// value y0 at x0
static double Gill(double x0, double y0,
                   double x, double h)
{
     
    // Count number of iterations
    // using step size or height h
    int n = (int)((x - x0) / h);
 
    // Value of K_i
    double k1, k2, k3, k4;
 
    // Initial value of y(0)
    double y = y0;
 
    // Iterate for number of iteration
    for(int i = 1; i <= n; i++)
    {
         
       // Apply Gill's Formulas to
       // find next value of y
        
       // Value of K1
       k1 = h * dydx(x0, y);
        
       // Value of K2
       k2 = h * dydx(x0 + 0.5 * h,
                      y + 0.5 * k1);
        
       // Value of K3
       k3 = h * dydx(x0 + 0.5 * h,
                      y + 0.5 * (-1 + Math.sqrt(2)) *
                     k1 + k2 * (1 - 0.5 * Math.sqrt(2)));
        
       // Value of K4
       k4 = h * dydx(x0 + h,
                      y - (0.5 * Math.sqrt(2)) *
                     k2 + k3 * (1 + 0.5 * Math.sqrt(2)));
        
       // Find the next value of y(n+1)
       // using y(n) and values of K in
       // the above steps
       y = y + (1.0 / 6) * (k1 + (2 - Math.sqrt(2)) * 
                            k2 + (2 + Math.sqrt(2)) *
                            k3 + k4);
        
       // Update next value of x
       x0 = x0 + h;
    }
 
    // Return the final value of dy/dx
    return y;
}
 
// Driver Code
public static void main(String[] args)
{
    double x0 = 0, y = 3.0,
            x = 5.0, h = 0.2;
 
    System.out.printf("y(x) = %.6f", Gill(x0, y, x, h));
}
}
 
// This code is contributed by Amit Katiyar

Python3

# Python3 program to implement Gill's method
from math import sqrt
 
# A sample differential equation
# "dy/dx = (x - y)/2"
def dydx(x, y):
    return (x - y) / 2
 
# Finds value of y for a given x
# using step size h and initial
# value y0 at x0
def Gill(x0, y0, x, h):
     
    # Count number of iterations
    # using step size or height h
    n = ((x - x0) / h)
 
    # Initial value of y(0)
    y = y0
 
    # Iterate for number of iteration
    for i in range(1, int(n + 1), 1):
         
        # Apply Gill's Formulas to
        # find next value of y
 
        # Value of K1
        k1 = h * dydx(x0, y)
 
        # Value of K2
        k2 = h * dydx(x0 + 0.5 * h, 
                       y + 0.5 * k1)
 
        # Value of K3
        k3 = h * dydx(x0 + 0.5 * h,
                       y + 0.5 * (-1 + sqrt(2)) *
                      k1 + k2 * (1 - 0.5 * sqrt(2)))
 
        # Value of K4
        k4 = h * dydx(x0 + h, y - (0.5 * sqrt(2)) *
                    k2 + k3 * (1 + 0.5 * sqrt(2)))
 
        # Find the next value of y(n+1)
        # using y(n) and values of K in
        # the above steps
        y = y + (1 / 6) * (k1 + (2 - sqrt(2)) *
                           k2 + (2 + sqrt(2)) *
                           k3 + k4)
 
        # Update next value of x
        x0 = x0 + h
 
    # Return the final value of dy/dx
    return y
 
# Driver Code
if __name__ == '__main__':
     
    x0 = 0
    y = 3.0
    x = 5.0
    h = 0.2
 
    print("y(x) =", round(Gill(x0, y, x, h), 6))
 
# This code is contributed by Surendra_Gangwar

C#

// C# program to implement Gill's method
using System;
 
class GFG{
  
// A sample differential equation
// "dy/dx = (x - y)/2"
static double dydx(double x, double y)
{
    return (x - y) / 2;
}
  
// Finds value of y for a given x
// using step size h and initial
// value y0 at x0
static double Gill(double x0, double y0,
                   double x, double h)
{
      
    // Count number of iterations
    // using step size or height h
    int n = (int)((x - x0) / h);
  
    // Value of K_i
    double k1, k2, k3, k4;
  
    // Initial value of y(0)
    double y = y0;
  
    // Iterate for number of iteration
    for(int i = 1; i <= n; i++)
    {
          
       // Apply Gill's Formulas to
       // find next value of y
         
       // Value of K1
       k1 = h * dydx(x0, y);
         
       // Value of K2
       k2 = h * dydx(x0 + 0.5 * h,
                      y + 0.5 * k1);
         
       // Value of K3
       k3 = h * dydx(x0 + 0.5 * h,
                      y + 0.5 * (-1 + Math.Sqrt(2)) *
                     k1 + k2 * (1 - 0.5 * Math.Sqrt(2)));
         
       // Value of K4
       k4 = h * dydx(x0 + h,
                      y - (0.5 * Math.Sqrt(2)) *
                     k2 + k3 * (1 + 0.5 * Math.Sqrt(2)));
         
       // Find the next value of y(n+1)
       // using y(n) and values of K in
       // the above steps
       y = y + (1.0 / 6) * (k1 + (2 - Math.Sqrt(2)) * 
                            k2 + (2 + Math.Sqrt(2)) *
                            k3 + k4);
         
       // Update next value of x
       x0 = x0 + h;
    }
  
    // Return the final value of dy/dx
    return y;
}
  
// Driver Code
public static void Main(String[] args)
{
    double x0 = 0, y = 3.0,
            x = 5.0, h = 0.2;
  
    Console.Write("y(x) = {0:F6}", Gill(x0, y, x, h));
}
}
 
// This code is contributed by Amit Katiyar

Javascript

<script>
 
// Javascript program to implement Gill's method 
 
// A sample differential equation
// "dy/dx = (x - y)/2"
function dydx(x, y)
{
    return (x - y) / 2;
}
   
// Finds value of y for a given x
// using step size h and initial
// value y0 at x0
function Gill(x0, y0, x, h)
{
       
    // Count number of iterations
    // using step size or height h
    let n = ((x - x0) / h);
   
    // Value of K_i
    let k1, k2, k3, k4;
   
    // Initial value of y(0)
    let y = y0;
   
    // Iterate for number of iteration
    for(let i = 1; i <= n; i++)
    {
           
       // Apply Gill's Formulas to
       // find next value of y
          
       // Value of K1
       k1 = h * dydx(x0, y);
          
       // Value of K2
       k2 = h * dydx(x0 + 0.5 * h,
                      y + 0.5 * k1);
          
       // Value of K3
       k3 = h * dydx(x0 + 0.5 * h,
                      y + 0.5 * (-1 + Math.sqrt(2)) *
                     k1 + k2 * (1 - 0.5 * Math.sqrt(2)));
          
       // Value of K4
       k4 = h * dydx(x0 + h,
                      y - (0.5 * Math.sqrt(2)) *
                     k2 + k3 * (1 + 0.5 * Math.sqrt(2)));
          
       // Find the next value of y(n+1)
       // using y(n) and values of K in
       // the above steps
       y = y + (1.0 / 6) * (k1 + (2 - Math.sqrt(2)) * 
                            k2 + (2 + Math.sqrt(2)) *
                            k3 + k4);
          
       // Update next value of x
       x0 = x0 + h;
    }
   
    // Return the final value of dy/dx
    return y;
}
 
// Driver Code
     
    let x0 = 0, y = 3.0,
            x = 5.0, h = 0.2;
   
    document.write("y(x) = ", Gill(x0, y, x, h).toFixed(6));
         
</script>

Output:

y(x) = 3.410426

Time Complexity: O(n^3/2)

Auxiliary Space: O(1)

Suggest improvement

Program to check if N is a Centered Tridecagonal Number

Find the length of the Largest subset such that all elements are Pairwise Coprime

Share your thoughts in the comments

Gill’s 4th Order Method to solve Differential Equations

C++

Java

Python3

C#

Javascript

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?