An algebraic identity is an equality that holds for any value of its variables. They are generally used in the factorization of polynomials or simplification of algebraic calculations. A polynomial is just a bunch of algebraic terms added together, for example, p(x) = 4x + 1 is a degree-1 polynomial. Similarly, polynomials can be of any degree 1, 2, 3… and so on. Polynomials are basically those Mathematical Expressions that make calculations easy in real life. There are different types of polynomials depending upon the number of terms present in them, for example, if there are 2 terms, it is known as a binomial.
Zeros of Polynomials
Let’s assume that P(x) is a polynomial. Let x = r, be the value of x where our polynomial P(x) becomes zero i.e,
P(x) = 0 at x = r or P(r) = 0
The process of finding the zeroes of P(x) is simply solving the equation P(x) = 0. We already know how to calculate zeros for first and second-degree polynomials. Let’s see some examples for this,
Question 1: P(x) = x2 + 2x – 15. Find the roots of this polynomial.
Solution:
Let’s put P(x) = 0,
x2 + 2x -15 = 0
⇒ x2 + 5x – 3x – 15 = 0
⇒ x(x +5) -3 (x + 5) = 0
⇒ (x – 3) (x + 5) = 0
So, this expression will be zero for two values of x, i.e. x = 3 and -5.
The last example used the factorization method for finding the roots of the polynomial. We can also use other methods such as the zero factor of the Shree Dharacharya Quadratic formula for finding out the roots or zeros of a polynomial.
If ax2 + bx + c = 0, where a≠0, then the formula for roots will be,
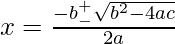
This formula for finding out roots of a polynomial is known as Shree Dharacharya Quadratic Formula.
Question 2: Solve for the roots of the polynomial, x2 + 6x – 14 = 0
Solution:
As it is clear that the above expression cannot be simplified just by intuition, therefore, we shall go for the Dharacharya Formula.
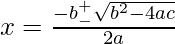
Here, a=1, b=+6, c=-14
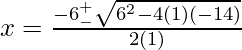
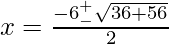
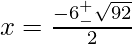
x=-3±√23
Geometric Meaning of Zeros of a Polynomial
We know what zeros are, but why are they important? Let’s look at the graphical interpretation of the meaning behind zeros. Let’s look at the graphs of first and second-degree polynomials.
Let’s take a polynomial y = 2x + 1, this is also an equation of a straight line. The figure below represents the graph of this straight line. We will look at the positions where y becomes zero.

This graph intersects the x-axis at one position, there is only one root. So, we can conclude from the graph that roots are the position where the graph of polynomial intersects the x-axis.
So, in general, for a polynomial y = ax + b, it represents a straight line with one root, which lies on the position where the graph cuts the x-axis i.e (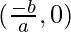 .
.
Now, let’s look at graphs of second-degree polynomials
Let p(x) = x2 – 3x – 4, the figure below represents its graph. Let’s focus on the roots of this polynomial.

In this graph, we can see that it cuts the x-axis at two points. So, these two points are the zeros of this polynomial. But will it be always this case? This graph can be upward facing or downward-facing depending upon the coefficient of x2.
In general, the zeroes of a quadratic polynomial ax2 + bx + c, a ≠ 0, are precisely the x-coordinates of the points where the parabola representing y = ax2 + bx + c intersects the x-axis.
Three possible cases can happen to the shape of the graph.
Case (i): The graph cuts the x-axis at two distinct points A and A′. This is the case that’s been shown above. Here the polynomial y = ax2 + bx + c has two distinct roots.
Case (ii): The graph cuts the x-axis at exactly one point, i.e., at two coincident points. Two same roots. Here the polynomial y = ax2 + bx + c has only one root.

Case (iii): The graph is either completely above x-axis or completely below the x-axis. Here the polynomial y = ax2 + bx + c has no roots.

Similarly, let’s study this for a cubic polynomial.
Cubic Polynomial
Let’s assume a polynomial, P(x) = x3 – 4x.
P(x) = x(x2-4)
= x(x-2)(x+2)
So the roots of this polynomial are x = 0, 2, -2.
We can verify from the graph that these must be the places where the curve cuts the x-axis.

But as in the case of second-degree polynomials, there may be more than one possibility.
Let’s take an example of cubic polynomial P(x) = x3

This graph cuts the x-axis only at one point. So, x = 0 is the only root of the polynomial p(x) = x3.
There can be another case, for example, take P(x) = x3 – x2.

We can see that the graph of this function cuts the x-axis at two places only. From the above example, we can say that this polynomial can have at most 3 zeros.
Note: In general a polynomial of degree “N” can have at most N zeros.
Question 1: Which of the following graphs represents a cubic polynomial.

Answer:
(A) is the graph of a cubic polynomial because it cuts the x-axis only three times.
(B) does not cut the x-axis at all and is continuously increasing, So it cannot be.
(C) It cuts the x-axis at more than 5 points. So it cannot be three degree polynomial
(D) It is a graph of a parabola, we studied earlier. So it is not a cubic polynomial.
Question 2: Show the zeros of the Quadratic equation on the graph, x2 – 3x – 4 = 0
Solution:
From the equation, we can tell that there are 2 values of x.
Factorizing the quadratic equation to find out the values of x,
x2-4x+x-4= 0
x(x-4) +1(x-4)= 0
x = (-1), x = 4
Hence, the graph will be an upward parabola intersecting at (-1,0) and (4,0)

Question 3: Find the point where the graph intersects x-axis for the quadratic equation, x2 – 2x – 8 = 0
Solution:
Factorize the quadratic equation to find the points,
x2-4x+2x-8 = 0
x(x-4) +2(x-4)= 0
(x-4)(x+2)= 0
x = 4, x = (-2)
Therefore, the equation will cut the graph on x-axis at (4,0) and (-2,0)

Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...