Generate Quadratic Equation having given sum and product of roots

Given two integers S and M, the task is to find the coefficients of the quadratic equation such that the sum and the product of the roots are S and M respectively.

Examples:

Input: S = 5, M = 6
Output: 1 -5 6
Explanation:
For the quadratic equation x² – 5x + 6 = 0. The root of the equation are 2 and 3. Therefore, the sum of roots is 2 + 3 = 5, and the product of roots is 2*3 = 6.

Input: S = -2, M = 1
Output: 1 2 1

Approach: The given problem can be solved by using the property of the Quadratic Equation as shown below:

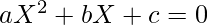
For the above quadratic equation the roots are given by:

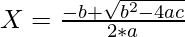 and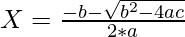 

The sum of roots is given by:

=> 
=> 
=> 

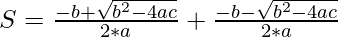
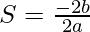
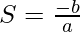
The product of roots is given by:

=> 
=> 

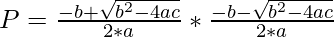
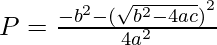
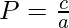
From the above two equations, if the value of a is 1 then the value of b is (-1)*S, and c is P. Therefore, the equation is given by:

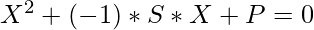
Below is the implementation of the above approach:

C++

// C++ program for the above approach

#include <bits/stdc++.h>
using namespace std;

// Function to find the quadratic
// equation from the given sum and
// products of roots
void findEquation(int S, int M)
{
    // Print the coefficients
    cout << "1 " << (-1) * S << " "
         << M << endl;
}

// Driver Code
int main()
{
    int S = 5, M = 6;
    findEquation(S, M);

    return 0;
}

Java

// Java program for the above approach
import java.io.*;

class GFG{

// Function to find the quadratic
// equation from the given sum and
// products of roots
public static void findEquation(int S, int M)
{

    // Print the coefficients
    System.out.println("1 " + ((-1) * S) + " " + M);
}

// Driver code
public static void main(String[] args)
{
      int S = 5, M = 6;

    findEquation(S, M);
}
}

// This code is contributed by user_qa7r

Python3

# Python3 program for the above approach

# Function to find the quadratic
# equation from the given sum and
# products of roots
def findEquation(S, M):

    # Print the coefficients
    print("1 ", ((-1) * S), " " , M)

# Driver Code
S = 5
M = 6

findEquation(S, M)

# This code is contributed by Ankita saini

C#

// C# program for the above approach
using System;

class GFG{

// Function to find the quadratic
// equation from the given sum and
// products of roots
public static void findEquation(int S, int M)
{

    // Print the coefficients
    Console.Write("1 " + ((-1) * S) + " " + M);
}

// Driver code
static void Main()
{
    int S = 5, M = 6;

    findEquation(S, M);
}
}

// This code is contributed by code_hunt

Javascript

<script>

// Javascript program for the above approach

// Function to find the quadratic
// equation from the given sum and
// products of roots
function findEquation(S, M)
{

    // Print the coefficients
    document.write("1 " + ((-1) * S) + " " + M);
}

// Driver Code
var S = 5, M = 6;

findEquation(S, M);

// This code is contributed by Ankita saini

</script>

Output:

1 -5 6

Time Complexity: O(1)
Auxiliary Space: O(1)