Given a single integer n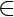 
[1, 1000000000], generate a Pythagoras triplet that includes n as one of its sides if possible.
Examples :
Input : 22
Output : Pythagoras Triplets exist i.e. 22 120 122
Input : 4
Output : Pythagoras Triplets exist i.e. 4 3 5
Input : 2
Output : No Pythagoras Triplet exists
Explanation:
Definition: “Pythagorean triplets” are integer solutions to the Pythagorean Theorem, i.e. they satisfy the equation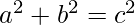 
Our task is to generate a triplet from an integral value. This can be a confusing task because, the side given to us can be a hypotenuse or a non-hypotenuse side.
Starting to calculate triplets by putting them in a formula, it can be deduced that only for 1 and 2, no triplets are possible.
Further,
if n is even, our triplets are calculated by formula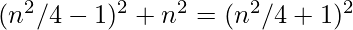 
if n is odd, our triplets are calculated by formula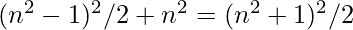 
Proof:
Pythagoras’s Theorem can also be written as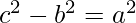 
i.e a*a = (c-b)(c+b)
a*a x 1 = a*a, thus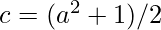 
and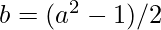 
, this solution works if n is odd.
For even solution,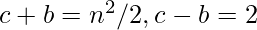 
, thus, we get the above formula when n is even.
Below is the implementation:
C++
#include <bits/stdc++.h>
using namespace std;
void evaluate(long long int n)
{
if (n == 1 || n == 2)
printf("No Pythagoras Triplet exists");
else if (n % 2 == 0) {
long long int var = 1LL * n * n / 4;
printf("Pythagoras Triplets exist i.e. ");
printf("%lld %lld %lld", n, var - 1, var + 1);
}
else if (n % 2 != 0) {
long long int var = 1LL * n * n + 1;
printf("Pythagoras Triplets exist i.e. ");
printf("%lld %lld %lld", n, var / 2 - 1, var / 2);
}
}
int main()
{
long long int n = 22;
evaluate(n);
return 0;
}
|
Java
import java.io.*;
class GFG
{
static void evaluate( int n)
{
if (n == 1 || n == 2)
System.out.println("No Pythagoras " +
"Triplet exists");
else if (n % 2 == 0)
{
int var = 1 * n * n / 4;
System.out.print("Pythagoras Triplets " +
"exist i.e. ");
System.out.print(n + " ");
System.out.print(var - 1+ " ");
System.out.println(var + 1 +" ");
}
else if (n % 2 != 0)
{
int var = 1 * n * n + 1;
System.out.print("Pythagoras Triplets " +
"exist i.e. ");
System.out.print(n + " ");
System.out.print(var / 2 - 1 + " ");
System.out.println(var / 2 + " ");
}
}
public static void main(String[] args)
{
int n = 22;
evaluate(n);
}
}
|
Python3
def evaluate(n):
if (n == 1 or n == 2):
print("No Pythagoras" +
" Triplet exists");
elif (n % 2 == 0):
var = n * n / 4;
print("Pythagoras Triplets" +
" exist i.e. ", end = "");
print(int(n), " ", int(var - 1),
" ", int(var + 1));
elif (n % 2 != 0):
var = n * n + 1;
print("Pythagoras Triplets " +
"exist i.e. ", end = "");
print(int(n), " ", int(var / 2 - 1),
" ", int(var / 2));
n = 22;
evaluate(n);
|
C#
using System;
class GFG
{
static void evaluate(int n)
{
if (n == 1 || n == 2)
Console.WriteLine("No Pythagoras " +
"Triplet exists");
else if (n % 2 == 0)
{
int var = 1 * n * n / 4;
Console.Write("Pythagoras Triplets " +
"exist i.e. ");
Console.Write(n + " ");
Console.Write(var - 1+ " ");
Console.WriteLine(var + 1 +" ");
}
else if (n % 2 != 0)
{
int var = 1 * n * n + 1;
Console.Write("Pythagoras Triplets " +
"exist i.e. ");
Console.Write(n + " ");
Console.Write(var / 2 - 1 + " ");
Console.WriteLine(var / 2 + " ");
}
}
static public void Main ()
{
int n = 22;
evaluate(n);
}
}
|
PHP
<?php
function evaluate($n)
{
if ($n == 1 || $n == 2)
echo "No Pythagoras Triplet exists";
else if ($n % 2 == 0) {
$var = $n * $n / 4;
echo "Pythagoras Triplets exist i.e. ";
echo $n, " ", $var - 1, " ", $var + 1;
}
else if ($n % 2 != 0) {
$var = $n * $n + 1;
echo "Pythagoras Triplets exist i.e. ";
echo $n, " ", $var / 2 - 1, " ", $var / 2;
}
}
$n = 22;
evaluate($n);
?>
|
Javascript
<script>
function evaluate(n)
{
if (n == 1 || n == 2)
document.write("No Pythagoras Triplet exists");
else if (n % 2 == 0)
{
let Var = 1 * n * n / 4;
document.write("Pythagoras Triplets " +
"exist i.e. ");
document.write(n + " ");
document.write(Var - 1+ " ");
document.write(Var + 1 +" ");
}
else if (n % 2 != 0)
{
let Var = 1 * n * n + 1;
document.write("Pythagoras Triplets " +
"exist i.e. ");
document.write(n + " ");
document.write(parseInt(Var / 2, 10) - 1 + " ");
document.write(parseInt(Var / 2, 10) + " ");
}
}
let n = 22;
evaluate(n);
</script>
|
OutputPythagoras Triplets exist i.e. 22 120 122
Time Complexity: O(1)
Auxiliary Space: O(1)