Generate all passwords from given character set

Given a set of characters generate all possible passwords from them. This means we should generate all possible permutations of words using the given characters, with repetitions and also upto a given length. 
Examples:

Input : arr[] = {a, b}, 
          len = 2.
Output :
a b aa ab ba bb

The solution is to use recursion on the given character array. The idea is to pass all possible lengths and an empty string initially to a helper function. In the helper function we keep appending all the characters one by one to the current string and recur to fill the remaining string till the desired length is reached.
It can be better visualized using the below recursion tree:

        (a, b)
         /   \
        a     b
       / \   / \
      aa  ab ba bb

Following is the implementation of the above method.

C++

// C++ program to generate all passwords for given characters
#include <bits/stdc++.h>
using namespace std;

// int cnt;

// Recursive helper function, adds/removes characters
// until len is reached
void generate(char* arr, int i, string s, int len)
{
    // base case
    if (i == 0) // when len has been reached
    {
        // print it out
        cout << s << "\n";
        // cnt++;
        return;
    }

    // iterate through the array
    for (int j = 0; j < len; j++) {

        // Create new string with next character
        // Call generate again until string has
        // reached its len
        string appended = s + arr[j];
        generate(arr, i - 1, appended, len);
    }

    return;
}

// function to generate all possible passwords
void crack(char* arr, int len)
{
    // call for all required lengths
    for (int i = 1; i <= len; i++) {
        generate(arr, i, "", len);
    }
}

// driver function
int main()
{
    char arr[] = { 'a', 'b', 'c' };
    int len = sizeof(arr) / sizeof(arr[0]);
    crack(arr, len);

    //cout << cnt << endl;
    return 0;
}
// This code is contributed by Satish Srinivas.

Java

// Java program to generate all passwords for given characters
import java.util.*;

class GFG
{

    // int cnt;
    // Recursive helper function, adds/removes characters
    // until len is reached
    static void generate(char[] arr, int i, String s, int len)
    {
        // base case
        if (i == 0) // when len has been reached
        {
            // print it out
            System.out.println(s);

            // cnt++;
            return;
        }

        // iterate through the array
        for (int j = 0; j < len; j++)
        {

            // Create new string with next character
            // Call generate again until string has
            // reached its len
            String appended = s + arr[j];
            generate(arr, i - 1, appended, len);
        }

        return;
    }

    // function to generate all possible passwords
    static void crack(char[] arr, int len)
    {
        // call for all required lengths
        for (int i = 1; i <= len; i++)
        {
            generate(arr, i, "", len);
        }
    }

    // Driver code
    public static void main(String[] args)
    {
        char arr[] = {'a', 'b', 'c'};
        int len = arr.length;
        crack(arr, len);
    }

}

// This code has been contributed by 29AjayKumar

Python 3

# Python3 program to
# generate all passwords
# for given characters

# Recursive helper function,
# adds/removes characters
# until len is reached
def generate(arr, i, s, len):

    # base case
    if (i == 0): # when len has
                 # been reached

        # print it out
        print(s)
        return

    # iterate through the array
    for j in range(0, len):

        # Create new string with
        # next character Call
        # generate again until
        # string has reached its len
        appended = s + arr[j]
        generate(arr, i - 1, appended, len)

    return

# function to generate
# all possible passwords
def crack(arr, len):

    # call for all required lengths
    for i in range(1 , len + 1):
        generate(arr, i, "", len)

# Driver Code
arr = ['a', 'b', 'c' ]
len = len(arr)
crack(arr, len)

# This code is contributed by Smita.

C#

// C# program to generate all passwords for given characters
using System;

class GFG
{

    // int cnt;
    // Recursive helper function, adds/removes characters
    // until len is reached
    static void generate(char[] arr, int i, String s, int len)
    {
        // base case
        if (i == 0) // when len has been reached
        {
            // print it out
            Console.WriteLine(s);

            // cnt++;
            return;
        }

        // iterate through the array
        for (int j = 0; j < len; j++)
        {

            // Create new string with next character
            // Call generate again until string has
            // reached its len
            String appended = s + arr[j];
            generate(arr, i - 1, appended, len);
        }

        return;
    }

    // function to generate all possible passwords
    static void crack(char[] arr, int len)
    {
        // call for all required lengths
        for (int i = 1; i <= len; i++)
        {
            generate(arr, i, "", len);
        }
    }

    // Driver code
    public static void Main(String[] args)
    {
        char []arr = {'a', 'b', 'c'};
        int len = arr.Length;
        crack(arr, len);
    }

}

/* This code contributed by PrinciRaj1992 */

Javascript

<script>
// JavaScript program to generate all passwords for given characters

    // let cnt;
    // Recursive helper function, adds/removes characters
    // until len is reached
    function generate(arr, i, s, len)
    {
        // base case
        if (i == 0) // when len has been reached
        {
            // print it out
            document.write(s + "<br/>");

            // cnt++;
            return;
        }

        // iterate through the array
        for (let j = 0; j < len; j++)
        {

            // Create new string with next character
            // Call generate again until string has
            // reached its len
            let appended = s + arr[j];
            generate(arr, i - 1, appended, len);
        }

        return;
    }

    // function to generate all possible passwords
    function crack(arr, len)
    {
        // call for all required lengths
        for (let i = 1; i <= len; i++)
        {
            generate(arr, i, "", len);
        }
    }


// Driver Code

        let arr = ['a', 'b', 'c'];
        let len = arr.length;
        crack(arr, len);

</script>

Output

a
b
c
aa
ab
ac
ba
bb
bc
ca
cb
cc
aaa
aab
aac
aba
abb
abc
aca
acb
acc
baa
bab
bac
bba
bbb
bbc
bca
bcb
bcc
caa
cab
cac
cba
cbb
cbc
cca
ccb
ccc

If we want to see the count of the words, we can uncomment the lines having cnt variable in the code. We can observe that it comes out to be 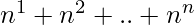, where n = len. Thus the time complexity of the program is also , hence exponential. We can also check for a particular password 
while generating and break the loop and return if it is found. We can also include other symbols to be generated and if needed remove duplicates by preprocessing the input using a HashTable.

 Approach#2: Using itertools

The approach used in this code is to generate all possible passwords of length up to ‘length’ using the characters in the array ‘arr’. The itertools.product() method is used to generate all possible combinations of length up to ‘length’ of the characters in ‘arr’, and the extend() method is used to add these combinations to the ‘passwords’ list.

Algorithm

1. Initialize an empty list ‘passwords’.
2. For i in range(1, length+1):
a. Generate all possible combinations of length i of the characters in ‘arr’ using itertools.product() method.
b. Convert each combination to a string using the join() method.
c. Add these strings to the ‘passwords’ list using the extend() method.
3. Return the ‘passwords’ list.

Python3

import itertools

def generate_passwords(arr, length):
    passwords = []
    for i in range(1, length+1):
        passwords.extend([''.join(x) for x in itertools.product(arr, repeat=i)])
    return passwords
arr = ['a', 'b', 'c' ]
length = len(arr)
print(generate_passwords(arr, length))

Output

['a', 'b', 'c', 'aa', 'ab', 'ac', 'ba', 'bb', 'bc', 'ca', 'cb', 'cc', 'aaa', 'aab', 'aac', 'aba', 'abb', 'abc', 'aca', 'acb', 'acc', 'baa', 'bab', 'bac', 'bba', 'bbb', 'bbc', 'bca', 'bcb', 'bcc', 'caa', 'cab', 'cac', 'cba', 'cbb', 'cbc', 'cca', 'ccb', 'ccc']

Time complexity: O(n^m), where n is the length of ‘arr’ and m is the maximum length of the password. This is because the itertools.product() method generates all possible combinations of length up to ‘length’ of the characters in ‘arr’, and there can be n^m such combinations.

Space complexity: O(n^m), because the ‘passwords’ list will contain n^m elements at most, and each element can have a length of up to m. Additionally, the itertools.product() method generates all possible combinations of length up to ‘length’ of the characters in ‘arr’, which can also take up space. However, the space used by itertools.product() is negligible compared to the space used by the ‘passwords’ list.