Generate elements of the array following given conditions
Last Updated :
31 May, 2022
Given an integer N, for every integer i in the range 2 to N, assign a positive integer 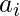 such that the following conditions hold :
such that the following conditions hold :
- For any pair of indices (i, j), if i and j are coprime then
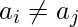 .
. - The maximum value of all
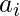 should be minimized (i.e. max value should be as small as possible).
should be minimized (i.e. max value should be as small as possible).
A pair of integers is called coprime if their gcd(i, j) = 1.
Examples:
Input: N = 4
Output: 1 2 1
Input: N = 10
Output: 1 2 1 3 2 4 1 2 3
Approach: We have to keep two things in mind while assigning values at indices from 2 to n. First, for any pair (i, j), if i and j are coprime then we cannot assign the same value to this pair of indices. Second, we have to minimize the maximum value assigned to each index from 2 to n.
This can be achieved if distinct numbers are assigned to each prime because all primes are coprime to each other. Then assign values at all-composite positions the same as any of its prime divisors. This solution works as for any pair (i, j), i is given the same number of a divisor and so is j, so if they are coprime, they cannot be given the same number.
This approach can be implemented by making a small change when building the Sieve of Eratosthenes.
When we met a prime for the first time, then assign a unique smallest value to it and all of its multiples. This way, all prime indices should have unique values and all composite indices have valued the same as any of its prime divisors.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void specialSieve(int n)
{
int cnt = 0;
int prime[n + 1];
for (int i = 0; i <= n; i++)
prime[i] = 0;
for (int i = 2; i <= n; i++) {
if (!prime[i]) {
cnt++;
for (int j = i; j <= n; j += i)
prime[j] = cnt;
}
}
for (int i = 2; i <= n; i++)
cout << prime[i] << " ";
}
int main()
{
int n = 6;
specialSieve(n);
return 0;
}
|
Java
import java.io.*;
class GFG
{
static void specialSieve(int n)
{
int cnt = 0;
int prime[] = new int[n+1];
for (int i = 0; i <= n; i++)
prime[i] = 0;
for (int i = 2; i <= n; i++)
{
if (!(prime[i]>0))
{
cnt++;
for (int j = i; j <= n; j += i)
prime[j] = cnt;
}
}
for (int i = 2; i <= n; i++)
System.out.print(prime[i] + " ");
}
public static void main (String[] args)
{
int n = 6;
specialSieve(n);
}
}
|
Python3
def specialSieve(n) :
cnt = 0;
prime = [0]*(n + 1);
for i in range(2, n + 1) :
if (not prime[i]) :
cnt += 1;
for j in range(i, n + 1, i) :
prime[j] = cnt;
for i in range(2, n + 1) :
print(prime[i],end = " ");
if __name__ == "__main__" :
n = 6;
specialSieve(n);
|
C#
using System;
class GFG
{
static void specialSieve(int n)
{
int cnt = 0;
int []prime = new int[n+1];
for (int i = 0; i <= n; i++)
prime[i] = 0;
for (int i = 2; i <= n; i++)
{
if (!(prime[i] > 0))
{
cnt++;
for (int j = i; j <= n; j += i)
prime[j] = cnt;
}
}
for (int i = 2; i <= n; i++)
Console.Write(prime[i] + " ");
}
public static void Main ()
{
int n = 6;
specialSieve(n);
}
}
|
Javascript
<script>
function specialSieve(n)
{
let cnt = 0;
let prime = new Array(n + 1);
for (let i = 0; i <= n; i++)
prime[i] = 0;
for (let i = 2; i <= n; i++) {
if (!prime[i]) {
cnt++;
for (let j = i; j <= n; j += i)
prime[j] = cnt;
}
}
for (let i = 2; i <= n; i++)
document.write(prime[i] + " ");
}
let n = 6;
specialSieve(n);
</script>
|
Time Complexity: O(N Log N)
Auxiliary Space: O(N)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...