Generate all permutations of a string that follow given constraints

Given a string, generate all permutations of it that do not contain ‘B’ after ‘A’, i.e., the string should not contain “AB” as a substring.

Examples:

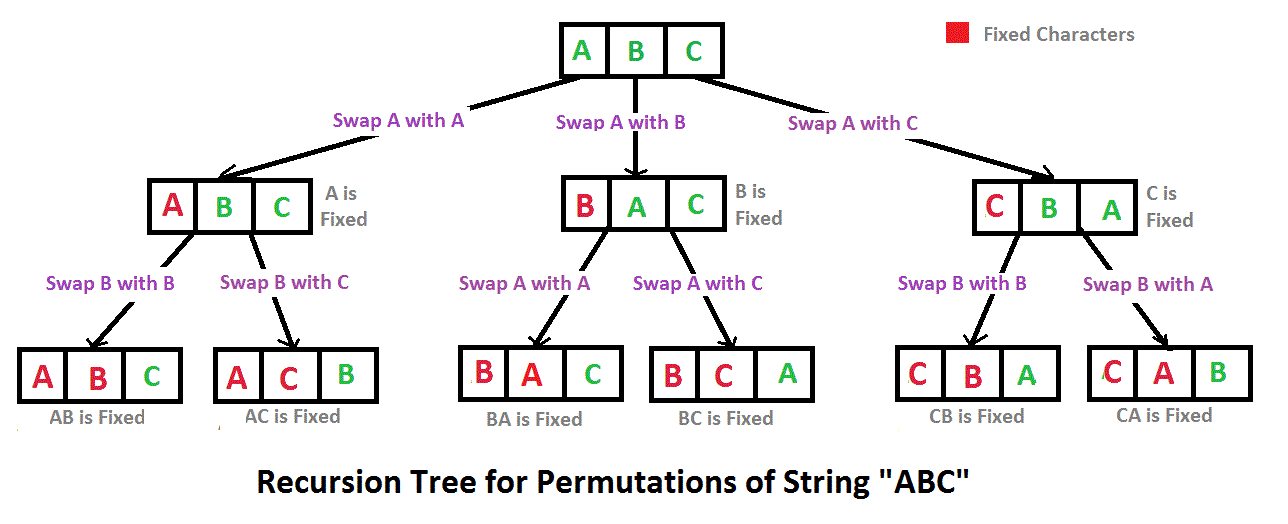
Input : str = “ABC” 
Output : ACB, BAC, BCA, CBA 
Out of 6 permutations of “ABC”, 4 follow the given constraint and 2 (“ABC” and “CAB”) do not follow. 

Input : str = “BCD” 
Output : BCD, BDC, CDB, CBD, DCB, DBC

A simple solution is to generate all permutations. For every permutation, check if it follows the given constraint.

C++

// Simple C++ program to print all permutations
// of a string that follow given constraint
#include <bits/stdc++.h>
using namespace std;

void permute(string& str, int l, int r)
{

    // Check if current permutation is
    // valid
    if (l == r) {
        if (str.find("AB") == string::npos)
            cout << str << " ";
        return;
    }

    // Recursively generate all permutation
    for (int i = l; i <= r; i++) {
        swap(str[l], str[i]);
        permute(str, l + 1, r);
        swap(str[l], str[i]);
    }
}

// Driver Code
int main()
{
    string str = "ABC";
    permute(str, 0, str.length() - 1);
    return 0;
}

Java

// Simple Java program to print all
// permutations of a String that
// follow given constraint
import java.util.*;

class GFG{

static void permute(char[] str, int l, int r)
{

    // Check if current permutation is
    // valid
    if (l == r)
    {
        if (!String.valueOf(str).contains("AB"))
            System.out.print(String.valueOf(str) + " ");
        return;
    }

    // Recursively generate all permutation
    for(int i = l; i <= r; i++)
    {
        char tmp = str[l];
        str[l] = str[i];
        str[i] = tmp;

        permute(str, l + 1, r);

        tmp = str[l];
        str[l] = str[i];
        str[i] = tmp;
    }
}

// Driver Code
public static void main(String[] args)
{
    String str = "ABC";

    permute(str.toCharArray(), 0,
            str.length() - 1);
}
}

// This code is contributed by Amit Katiyar

Python

# Simple Python program to print all permutations
# of a string that follow given constraint


def permute(str, l, r):

    # Check if current permutation is
    # valid
    if (l == r):
        if "AB" not in ''.join(str):
            print(''.join(str), end=" ")
        return

    # Recursively generate all permutation
    for i in range(l, r + 1):
        str[l], str[i] = str[i], str[l]
        permute(str, l + 1, r)
        str[l], str[i] = str[i], str[l]


# Driver Code
str = "ABC"
permute(list(str), 0, len(str) - 1)

# This code is contributed by SHUBHAMSINGH10

C#

// Simple C# program to print all permutations
// of a string that follow given constraint
using System;
using System.Text;

class GFG {

    static void permute(StringBuilder str, int l, int r)
    {

        // Check if current permutation is
        // valid
        if (l == r) {
            if (str.ToString().IndexOf("AB") == -1) {
                Console.Write(str.ToString() + " ");
            }

            return;
        }

        // Recursively generate all permutation
        for (int i = l; i <= r; i++) {
            char tmp = str[l];
            str[l] = str[i];
            str[i] = tmp;

            permute(str, l + 1, r);
            tmp = str[l];
            str[l] = str[i];
            str[i] = tmp;
        }
    }

    // Driver code
    static void Main(string[] arg)
    {
        string str = "ABC";
        StringBuilder s = new StringBuilder(str);

        permute(s, 0, str.Length - 1);
    }
}

// This code is contributed by rutvik_56

Javascript

<script>

// JavaScript code to implement the above approach
function permute(str, l, r)
{

    // Check if current permutation is
    // valid
    if (l == r) {
        if (str.indexOf("AB") == -1)
            document.write(str," ");
        return;
    }

    // Recursively generate all permutation
    for (let i = l; i <= r; i++) {
        let a = str.split("");
        let temp = a[l];
        a[l] = a[i];
        a[i] = temp;
        permute(a.join(""), l + 1, r);
        temp = a[l];
        a[l] = a[i];
        a[i] = temp;
    }
}

// Driver Code

let str = "ABC";
permute(str, 0, str.length - 1);

// This code is contributed by shinjanpatra

</script>

Output

ACB BAC BCA CBA 

Time Complexity: O(n! X n) where n! is the number of permutations generated and O(n) times to print a permutation. 

Auxiliary Space: O(n! X n )

The above solution first generates all permutations, then for every permutation, it checks if it follows given constraint or not. 

An efficient solution is to use Backtracking. We cut down the recursion tree whenever we see that substring “AB” is formed. How do we do this? we add a isSafe() function. Before doing a swap, we check if previous character is ‘A’ and current character is ‘B’.

Below is the implementation of the above code:

C++

// Backtracking based CPP program to print all
// permutations of a string that follow given
// constraint
#include <bits/stdc++.h>
using namespace std;

bool isSafe(string& str, int l, int i, int r)
{
    // If previous character was 'A' and character
    // is 'B', then do not proceed and cut down
    // the recursion tree.
    if (l != 0 && str[l - 1] == 'A' && str[i] == 'B')
        return false;

    // This condition is explicitly required for
    // cases when last two characters are "BA". We
    // do not want them to swapped and become "AB"
    if (r == l + 1 && str[i] == 'A' && str[l] == 'B'
        || r == l + 1 && l == i && str[r] == 'B'
               && str[l] == 'A')
        return false;

    return true;
}

void permute(string& str, int l, int r)
{
    // We reach here only when permutation
    // is valid
    if (l == r) {
        cout << str << " ";
        return;
    }

    // Fix all characters one by one
    for (int i = l; i <= r; i++) {

        // Fix str[i] only if it is a
        // valid move.
        if (isSafe(str, l, i, r)) {
            swap(str[l], str[i]);
            permute(str, l + 1, r);
            swap(str[l], str[i]);
        }
    }
}

// Driver Code
int main()
{
    string str = "ABC";

    // Function call
    permute(str, 0, str.length() - 1);
    return 0;
}

Java

// Backtracking based JAVA program
// to print all permutations of a
// string that follow given constraint

public class GFG
{
    public boolean isSafe(String str,
                          int l,
                          int i,
                          int r)
    {
        // If previous character was 'A'
        // and  character is 'B', then
        // do not proceed and cut down the
        // recursion tree.
        if (l != 0 && str.charAt(l - 1) == 'A'
            && str.charAt(i) == 'B')
            return false;

        // This condition is explicitly required
        // for cases when last two characters
        // are "BA". We do not want them to
        // swapped and become "AB"
        if (r == l + 1 && str.charAt(i) == 'A'
                      && str.charAt(l) == 'B'
                      || r == l + 1 && l == i
                      && str.charAt(r) == 'B'
                      && str.charAt(l) == 'A')
            return false;

        return true;
    }

    /**
     * permutation function
     * @param str string to calculate
       permutation for
     * @param l starting index
     * @param r end index
     */
    private void permute(String str,
                         int l, int r)
    {
        // We reach here only when permutation
        // is valid
        if (l == r)
            System.out.print(str + " ");
        else
        {
            // Fix all characters one by one
            for (int i = l; i <= r; i++)
            {
                // Fix str[i] only if it is a
                // valid move.
                if (isSafe(str, l, i, r))
                {
                    str = swap(str, l, i);
                    permute(str, l + 1, r);
                    str = swap(str, l, i);
                }
            }
        }
    }

    /**
     * Swap Characters at position
     * @param a string value
     * @param i position 1
     * @param j position 2
     * @return swapped string
     */
    public String swap(String a, int i, int j)
    {
        char temp;
        char[] charArray = a.toCharArray();
        temp = charArray[i];
        charArray[i] = charArray[j];
        charArray[j] = temp;
        return String.valueOf(charArray);
    }

    // Driver Code
    public static void main(String[] args)
    {
        String str = "ABC";
        int n = str.length();
        GFG permutation = new GFG();

        // Function call
        permutation.permute(str, 0, n - 1);
    }
}

Python

# Backtracking based Python3 program to print all
# permutations of a string that follow given
# constraint


def isSafe(str, l, i, r):

    # If previous character was 'A' and character
    # is 'B', then do not proceed and cut down
    # the recursion tree.
    if (l != 0 and str[l - 1] == 'A' and str[i] == 'B'):
        return False

    # This condition is explicitly required for
    # cases when last two characters are "BA". We
    # do not want them to swapped and become "AB"
    if (r == l + 1 and str[i] == 'A' and str[l] == 'B'
        or r == l + 1 and l == i and str[r] == 'B'
            and str[l] == 'A'):
        return False

    return True


def permute(str, l, r):

    # We reach here only when permutation
    # is valid
    if (l == r):
        print(*str, sep="", end=" ")
        return

    # Fix all characters one by one
    for i in range(l, r + 1):

        # Fix str[i] only if it is a
        # valid move.
        if (isSafe(str, l, i, r)):
            str[l], str[i] = str[i], str[l]
            permute(str, l + 1, r)
            str[l], str[i] = str[i], str[l]


# Driver Code
str = "ABC"

# Function call
permute(list(str), 0, len(str) - 1)

# This code is contributed by SHUBHAMSINGH10

C#

// Backtracking based C# program to print all
// permutations of a string that follow given
// constraint
using System;

public class GFG
{
    // Backtracking based C# program
    // to print all permutations of a
    // string that follow given constraint
    using System;
    using System.Text;

    class GFG {

        static bool isSafe(StringBuilder str,
                           int l, int i,
                           int r)
        {

            // If previous character was 'A'
            // and character is 'B', then do not
            // proceed and cut down the recursion tree.
            if (l != 0 && str[l - 1] == 'A'
                && str[i] == 'B')
                return false;

            // This condition is explicitly
            // required for cases when last two
            // characters are "BA". We do not want
            // them to swapped and become "AB"
            if (r == l + 1 && str[i] == 'A'
                && str[l] == 'B' || r == l + 1
                && l == i && str[r] == 'B'
                && str[l] == 'A')
                return false;

            return true;
        }

        static void permute(StringBuilder str,
                             int l, int r)
        {

            // We reach here only when permutation
            // is valid
            if (l == r)
            {
                Console.Write(str + " ");
                return;
            }

            // Fix all characters one by one
            for (int i = l; i <= r; i++)
            {

                // Fix str[i] only if it is a
                // valid move.
                if (isSafe(str, l, i, r))
                {
                    char temp = str[l];
                    str[l] = str[i];
                    str[i] = temp;
                    permute(str, l + 1, r);
                    temp = str[l];
                    str[l] = str[i];
                    str[i] = temp;
                }
            }
        }

        // Driver code
        static void Main()
        {
            string str = "ABC";
            StringBuilder s = new StringBuilder(str);

            // Function call
            permute(s, 0, str.Length - 1);
        }
    }

    // This code is contributed by divyeshrabadiya07

Javascript

const GFG = {
  isSafe(str, l, i, r) {
    // If previous character was 'A'
    // and  character is 'B', then
    // do not proceed and cut down the
    // recursion tree.
    if (l !== 0 && str[l - 1] === 'A' && str[i] === 'B') return false;

    // This condition is explicitly required
    // for cases when last two characters
    // are "BA". We do not want them to
    // swapped and become "AB"
    if ((r === l + 1 && str[i] === 'A' && str[l] === 'B')
        || (r === l + 1 && l === i && str[r] === 'B' && str[l] === 'A')) {
      return false;
    }

    return true;
  },
  permute(str, l, r) {
    // We reach here only when permutation
    // is valid
    if (l === r) console.log(`${str} `);
    else {
      // Fix all characters one by one
      for (let i = l; i <= r; i++) {
        // Fix str[i] only if it is a
        // valid move.
        if (this.isSafe(str, l, i, r)) {
          str = this.swap(str, l, i);
          this.permute(str, l + 1, r);
          str = this.swap(str, l, i);
        }
      }
    }
  },
  swap(a, i, j) {
    let temp;
    const charArray = a.split('');
    temp = charArray[i];
    charArray[i] = charArray[j];
    charArray[j] = temp;
    return charArray.join('');
  },
};

// Driver Code
const str = 'ABC';
const n = str.length;

// Function call
GFG.permute(str, 0, n - 1);

Output

ACB BAC BCA CBA