Generate a sequence with the given operations

Given a string 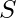which contains only 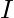(increase) and 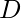(decrease). The task is to return any permutation of integers [0, 1, …, N] where N ≤ Length of S such that for all i = 0, …, N-1: 

1. If S[i] == “D”, then A[i] > A[i+1]
2. If S[i] == “I”, then A[i] < A[i+1].

Note that output must contain distinct elements.

Examples:

Input: S = “DDI” 
Output: [3, 2, 0, 1]

Input: S = “IDID” 
Output: [0, 4, 1, 3, 2] 

Approach:

If S[0] == “I”, then choose 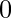as the first element. Similarly, if S[0] == “D”, then choose 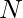as the first element. Now for every 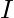operation, choose the next maximum element which hasn’t been chosen before from the range [0, N], and for the 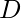operation, choose the next minimum.

Below is the implementation of the above approach:

C++

//C++ Implementation of above approach
#include<bits/stdc++.h>
using namespace std;
    // function to find minimum required permutation
    void  StringMatch(string s)
    {
    int lo=0, hi = s.length(), len=s.length();
    vector<int> ans;
    for (int x=0;x<len;x++)
    {
        if (s[x] == 'I')
        {
            ans.push_back(lo) ;
            lo += 1;
            }
        else
        {
            ans.push_back(hi) ;
            hi -= 1;
            }
    }
            ans.push_back(lo) ;
    cout<<"[";
    for(int i=0;i<ans.size();i++)
    {
    cout<<ans[i];
    if(i!=ans.size()-1)
    cout<<",";
    }
    cout<<"]";
}
// Driver code
int main()
{
string S = "IDID";
StringMatch(S);
return 0;
}
//contributed by Arnab Kundu

Java

// Java Implementation of above approach
import java.util.*;

class GFG
{

// function to find minimum required permutation
static void StringMatch(String s)
{
    int lo=0, hi = s.length(), len=s.length();
    Vector<Integer> ans = new Vector<>();
    for (int x = 0; x < len; x++)
    {
        if (s.charAt(x) == 'I')
        {
            ans.add(lo) ;
            lo += 1;
        }
        else
        {
            ans.add(hi) ;
            hi -= 1;
        }
    }
            ans.add(lo) ;
    System.out.print("[");
    for(int i = 0; i < ans.size(); i++)
    {
        System.out.print(ans.get(i));
        if(i != ans.size()-1)
            System.out.print(",");
    }
    System.out.print("]");
}

// Driver code
public static void main(String[] args)
{
    String S = "IDID";
    StringMatch(S);
}
}

// This code is contributed by Rajput-Ji

Python

# Python Implementation of above approach

# function to find minimum required permutation
def StringMatch(S):
    lo, hi = 0, len(S)
    ans = []
    for x in S:
        if x == 'I':
            ans.append(lo)
            lo += 1
        else:
            ans.append(hi)
            hi -= 1

    return ans + [lo]

# Driver code
S = "IDID"
print(StringMatch(S))

C#

// C# Implementation of above approach
using System;
using System.Collections.Generic;

class GFG
{

// function to find minimum required permutation
static void StringMatch(String s)
{
    int lo=0, hi = s.Length, len=s.Length;
    List<int> ans = new List<int>();
    for (int x = 0; x < len; x++)
    {
        if (s[x] == 'I')
        {
            ans.Add(lo) ;
            lo += 1;
        }
        else
        {
            ans.Add(hi) ;
            hi -= 1;
        }
    }
            ans.Add(lo) ;
    Console.Write("[");
    for(int i = 0; i < ans.Count; i++)
    {
        Console.Write(ans[i]);
        if(i != ans.Count-1)
            Console.Write(",");
    }
    Console.Write("]");
}

// Driver code
public static void Main(String[] args)
{
    String S = "IDID";
    StringMatch(S);
}
}

// This code is contributed by 29AjayKumar

Javascript

<script>

// Javascript implementation of above approach

// function to find minimum required permutation
    function  StringMatch(s)
    {
    var lo=0, hi = s.length, len=s.length;
    var ans=[];
    for (var x=0;x<len;x++)
    {
        if (s[x] == 'I')
        {
            ans.push(lo) ;
            lo += 1;
            }
        else
        {
            ans.push(hi) ;
            hi -= 1;
            }
    }
            ans.push(lo) ;
    document.write("[");
    for(var i=0;i<ans.length;i++)
    {
     document.write(ans[i]);
    if(i!=ans.length -1)
     document.write(", ");
    }
     document.write("]");
}

var S = "IDID";
StringMatch(S);


// This code is contributed by SoumikMondal

</script>

Output

[0,4,1,3,2]

Time Complexity: O(n), where n is the length of the given string.
Auxiliary Space: O(n), where n is the length of the given string.