Mathematics | Generalized PnC Set 1
Last Updated :
15 Dec, 2021
Prerequisite – PnC and Binomial Coefficients
So far every problem discussed in previous articles has had sets of distinct elements, but sometimes problems may involve repeated use of elements. This article covers such problems, where elements of the set are indistinguishable (or identical or not distinct).
Permutations with repetition –
Counting permutations when repetition of elements can be easily done using the product rule.
Example, number of strings of length 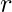 is
is 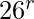 , since for every character there are 26 possibilities.
, since for every character there are 26 possibilities.
The number of 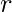 -permutations of a set of
-permutations of a set of 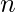 objects
with repetition is
objects
with repetition is 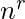 .
.
Combinations with repetition –
Counting the number of combinations with repetition is a bit more complicated than counting permutations. Consider a set of 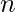 types of objects and we need to find out in how many ways can
types of objects and we need to find out in how many ways can 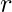 elements be chosen.
elements be chosen.
To solve the above problem we will first take a look at a similar problem that is arranging bars(|) and stars(*). Suppose there are 5 bars and 3 stars. One possible arrangement is –
||*||**|
They can be arranged in 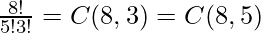 ways.
ways.
Our original problem is similar to the above problem. The bars represent divisions between the types of elements such that each type is separated by a bar and the number of stars is 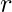 .
.
If a star is before the nth bar, then that means an item of nth type is selected, except for the last type where the star can be after a bar. For example, the arrangement mentioned above, ||*||**|, represents a selection of 1 element of 3rd type and 2 elements of 5th type.
In this way our original problem can be thought of as arranging 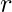 stars (elements) and
stars (elements) and 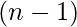 bars(divisions). The above result can be generalized as-
bars(divisions). The above result can be generalized as-
There are 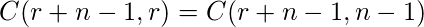
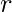 -combinations from a set with
-combinations from a set with 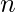 elements when repetition is allowed.
elements when repetition is allowed.
- Example 1 – In how many ways can 4 drinks can be chosen out of 6 possible types of drinks? There is no restriction on the number of drinks of a type that can be chosen and drinks of the same type are indistinguishable.
- Solution – The above scenario is a direct application of finding combinations with repetition. So the number of 4-combinations is –
 .
.
- Example 2 – How many solutions does the equation
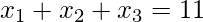 have, where
have, where 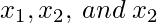 are non-negative integers?
are non-negative integers?
- Solution –
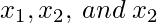 can have values ranging from 0 to 11. This situation is analogous to finding 11-combinations of 3 types of objects.
can have values ranging from 0 to 11. This situation is analogous to finding 11-combinations of 3 types of objects.
So number of solutions is –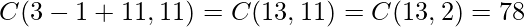
- Example 3 – Consider the same question as Example 2 but with the additional constraint that
 .
.
- Solution – Since the minimum value of
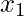 is 1, the effective equation becomes
is 1, the effective equation becomes 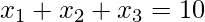 . So the number of solutions is-
. So the number of solutions is- 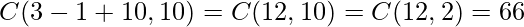
- Example 4 – Consider the same question as Example 2 but with the additional constraint that
 .
.
- Solution – Since the constraint is not a lower limit but an upper limit, it cannot be solved in the same way as in Example 3. There is another way of solving such problems.
For each type of object we assign a polynomial of the form – 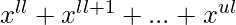 , where ‘ll’ and ‘ul’ are the lower and upper limits for that type of object.
, where ‘ll’ and ‘ul’ are the lower and upper limits for that type of object.
Then all such polynomials are multiplied and the coefficient of 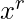 is the number of
is the number of 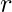 -combinations.
-combinations.
In our case, there is a constraint only on 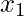 . Its polynomial therefore is-
. Its polynomial therefore is-
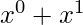
Polynomial for 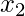 and
and 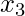 is-
is-
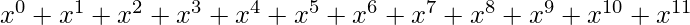
Since multiplying polynomials can be tedious, we use a trick which uses the binomial theorem.
The above polynomial can be extended to be an infinite series since the higher order terms won’t make any difference as we are only looking for the coefficient of 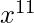 .
.
So the polynomial for 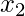 and
and 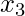 is-
is-
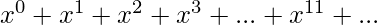
The above polynomial is also the expansion for 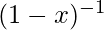 .
.
On multiplying the polynomials we get-
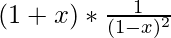
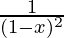 can be expanded through binomial theorem for negative exponents. We won’t need to expand the complete polynomial, as we just need the terms
can be expanded through binomial theorem for negative exponents. We won’t need to expand the complete polynomial, as we just need the terms 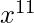 and
and 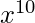 , because they will be multiplied by 1 and
, because they will be multiplied by 1 and 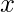 to get terms of
to get terms of 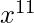 .
.
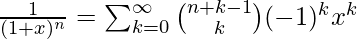 .
.
For  [Tex]k=10 [/Tex], we get-
[Tex]k=10 [/Tex], we get-
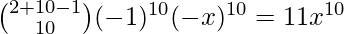
For  [Tex]k=11 [/Tex], we get-
[Tex]k=11 [/Tex], we get-
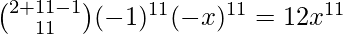
On multiplying the above obtained terms with 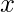 and 1 we get terms of
and 1 we get terms of 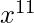 . On adding them up we get-
. On adding them up we get-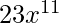 .
.
Therefore there are 23 solutions to the given equation.
- Example 5 – Consider the same question as in Example-2 but with an inequality i.e.
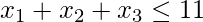 .
.
- Solution – We could solve this problem in 2 ways.
One way is to add up all 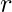 -combinations for values of
-combinations for values of 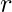 starting from 0 upto 11 i.e.
starting from 0 upto 11 i.e.
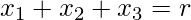 for
for 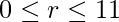 . We get the following values-
. We get the following values-
For 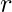 = 0, ways = C(3-1+0,2) = C(2,2) = 1
= 0, ways = C(3-1+0,2) = C(2,2) = 1
For 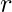 = 1, ways = C(3-1+1,2) = C(3,2) = 3
= 1, ways = C(3-1+1,2) = C(3,2) = 3
For 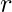 = 2, ways = C(3-1+2,2) = C(4,2) = 6
= 2, ways = C(3-1+2,2) = C(4,2) = 6
For 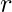 = 3, ways = C(3-1+3,2) = C(5,2) = 10
= 3, ways = C(3-1+3,2) = C(5,2) = 10
For 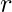 = 4, ways = C(3-1+4,2) = C(6,2) = 15
= 4, ways = C(3-1+4,2) = C(6,2) = 15
For 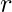 = 5, ways = C(3-1+5,2) = C(7,2) = 21
= 5, ways = C(3-1+5,2) = C(7,2) = 21
For 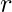 = 6, ways = C(3-1+6,2) = C(8,2) = 28
= 6, ways = C(3-1+6,2) = C(8,2) = 28
For 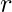 = 7, ways = C(3-1+7,2) = C(9,2) = 36
= 7, ways = C(3-1+7,2) = C(9,2) = 36
For 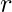 = 8, ways = C(3-1+8,2) = C(10,2) = 45
= 8, ways = C(3-1+8,2) = C(10,2) = 45
For 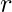 = 9, ways = C(3-1+9,2) = C(11,2) = 55
= 9, ways = C(3-1+9,2) = C(11,2) = 55
For 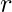 = 10, ways = C(3-1+10,2) = C(12,2) = 66
= 10, ways = C(3-1+10,2) = C(12,2) = 66
For 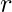 = 11, ways = C(3-1+11,2) = C(13,2) = 78
= 11, ways = C(3-1+11,2) = C(13,2) = 78
Total number of solutions = 364
The above problem is the same as finding the number of solutions for the equation-
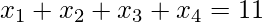
The extra variable can be thought of as the difference of 11 and 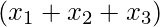 .
.
When 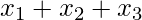 is 0,
is 0, 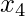 is 11. So
is 11. So 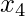 takes values accordingly.
takes values accordingly.
And the number of solutions of this equation is – C(4-1+11,4-1) = C(14,3) = 364.
References –
Permutations and Combinations
Discrete Mathematics and its Applications, by Kenneth H Rosen
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...