The binomial theorem or expansion describes the algebraic expansion of powers of a binomial. According to this theorem, it is possible to expand the polynomial “(a + b)n“ into a sum involving terms of the form “axzyc“, the exponents z and c are non-negative integers where z + c = n, and the coefficient of each term is a positive integer depending on the values of n and b.
Example: If n = 4
(a + b)4 = a4 + 4a3y + 6a2b2 + 4ab3 + b
General Term of Binomial Expansion
The General Term of Binomial Expansion of (x + y)n is as follows

- Tr+1 is the General Term in the binomial expansion
- The General term expansion is used to find the terms mentioned in the above formula.
- To find the terms in the binomial expansion we need to expand the given expansion.
- Suppose (a + b)n is the equation then the series of its binomial expansion will be as follows:
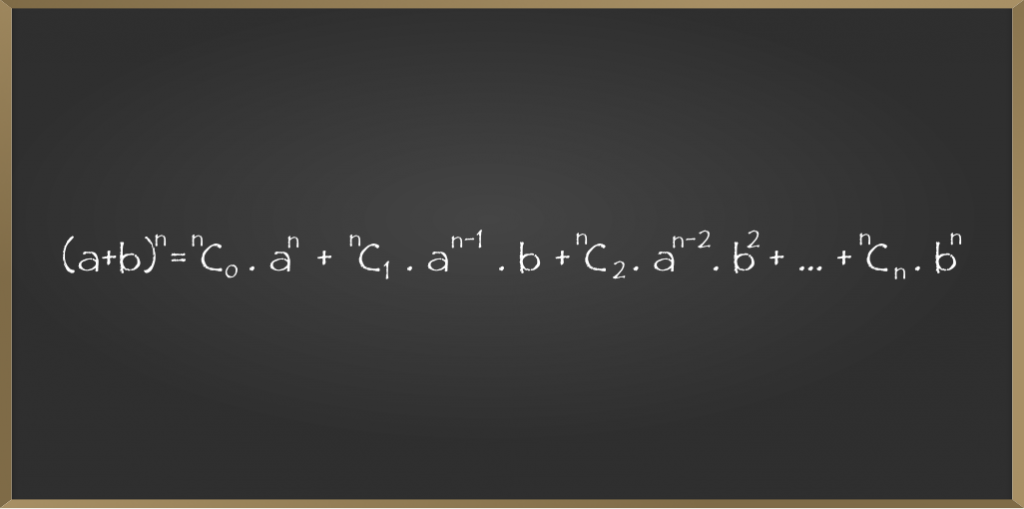
- The first term of the series is T1 = nC0.an
- The second term of the series is T2 = nC1.an-1.b
- The third term of the series is T3 = nC2.an-2.b2
- The nth term of the series is Tn= nCn.bn
Sample Problems on General Term
Example 1: Find (r+1)th term for the given binomial expansion (x + 2y)5
Solution:
Given expansion is (x + 2y)5
a = x, b= 2y, n = 5
The formula for (r+1)th is nCr .an – r.br
(r+1)th term =5Cr.x5 -r.2yr
Example 2: Find (r+1)th term for the given binomial expansion (a + 2b)7
Solution:
Given expansion is (a + 2b)7
a = a, b = 2b, n = 7
The formula for (r+1)th is nCr .an – r.br
(r+1)th term = 7Cr.a7 -r.br
Example 3: Find (r + 1)th term for the given binomial expansion (6p + 2q)12
Solution:
Given expansion is (6p + 2q)
a = 6p, b = 2q, n = 12
The formula for (r+1)th is nCr .an – r.br
(r + 1)th term = 12Cr.6p12 -r.2qr
Middle Term of the Binomial Expansion
If (x + y)n = nCr.xn – r.yr , it has (n + 1) terms and the middle term will depend upon the value of n.
We have two cases for the Middle Term of a Binomial Expansion:
If n is Even
If n is the even number then we make it into an odd number and consider (n + 1) as odd and (n/2 + 1) as the middle term. In simple, if n is even then we consider it as odd.
Suppose n is the even so, (n + 1) is odd. To find out the middle term :
Consider the general term of binomial expansion i.e.

- Now we replace “r ” with “n/2” in the above equation to find the middle term
- Tr+1 = Tn/2 + 1
- Tn/2 + 1 = nCn/2.xn – n/2.yn/2
Sample Problems on Middle Terms
Example 1: Find the middle of the following binomial expansion (x + a)8
Solution:
Given expansion is (x + a)8
n = 8, we consider the expansion has (n + 1) terms so the above expansion has (8 + 1) i.e 9 terms
we have T1, T2, T3, T4, T5, T6 , T7, T8, T9.
Tr+1 = Tn/2 + 1 = nCn/2.xn – n/2.Yn/2
T8/2 + 1 = 8C8/2.x8-8/2.a8/2
T5 = 8C4.x4.a4 is the required middle term of the given binomial expansion.
Example 2: Find the middle of the following binomial expansion (x + 3y)6
Solution:
Given expansion is (x + 3y)6
n = 6, we consider the expansion has (n + 1) terms so the above expansion has (6 + 1) i.e 7 terms
we have T1, T2, T3, T4, T5, T6 , T7.
Tr+1 = Tn/2 + 1 = nCn/2.xn – n/2.Yn/2
T6/2 + 1 = 6C6/2.x6-6/2.3y6/2
T4 = 6C3.x3.3y3 is the required middle term of the given binomial expansion.
Example 3: Find the middle of the following binomial expansion (2x + 5y)4
Solution:
Given expansion is (2x – 5y)4
n = 4, we consider the expansion has (n + 1) terms so the above expansion has (4 + 1) i.e 5 terms
we have T1, T2, T3, T4, T5.
Tr+1 = Tn/2 + 1 = nCn/2.xn – n/2.Yn/2
T4/2 + 1 = 4C4/2.2x4-4/2.5y4/2
T3 = 4C2.x2.5y2 is the required middle term of the given binomial expansion.
If n is Odd
If n is the odd number then we make it into an even number and consider (n + 1) as even and (n + 1/2), (n + 3/2) as the middle terms. In simple, if n is odd then we consider it even.
We have two middle terms if n is odd. To find the middle term:
Consider the general term of binomial expansion i.e

- In this case, we replace “r” with the two different values
- One term is (n + 1/2) compare with (r + 1) terms we get
r + 1 = n + 1/2
r = n + 1/2 -1
r = n -1/2
- Second middle term , compare (r + 1) with (n + 3/2) we get
r +1 = n +3/2
r = n + 3/2 – 1
r = n + 1/2
The two middle terms when n is odd are (n – 1/2) and (n + 1/2).
Sample Problems on Middle Terms
Example 1: Find the middle terms of the following binomial expansion (x + a)9
Solution:
Given expansion is (x + a)9
a = x, b = a, and n = 9
Middle terms will be (n – 1)/2 and (n + 1)/2
Tr + 1 =T n – 1/2 and Tn + 1/2
First middle term:
Tr + 1 = Tn – 1/2 = 9C(n – 1)/2.x9 – (n – 1)/2.a(n – 1)/2
T(9 – 1/2) = 9C(9 – 1)/2.x9 – (n – 1)/2.a(n – 1)/2
T4 = 9C4.x5.a4
Second middle term:
Tr + 1 = Tn + 1/2 = 9C(n + 1)/2.x9 – (n + 1)/2.a(n + 1)/2
T(9 + 1)/2 = 9C(9 + 1)/2.x9 – (9 + 1)/2.a(9 + 1)/2
T5 = 9C5.x4.a5
The middle terms of expansion are T4, and T5.
Example 2: Find the middle terms of the following binomial expansion (4a + 9b)7
Solution:
Given expansion is (4a + 9b)7
a = 4a,b = 9b, and n = 7
middle terms will be (n -1/2) and (n + 1/2)
Tr + 1 =T n – 1/2 and Tn + 1/2
First middle term:
Tr + 1 = Tn – 1/2 = 7C(n – 1)/2.4a7 – (n – 1)/2.9b(n – 1)/2
T(7 – 1/2) = 7C(7 – 1)/2.4a7 – (7 – 1)/2.9b(7 – 1)/2
T3 = 7C3.4a4.9b3
Second middle term:
Tr + 1 = T(n + 1)/2 = 7C(n + 1)/2.4a7 – (n + 1)/2.9b(n + 1)/2
T(7 + 1)/2 = 7C(7 + 1)/2.4a7 – (7 + 1)/2.9b(7 + 1)/2
T4 = 7C4.4a3.9b4
The middle terms of expansion are T3, and T4.
Example 3: Find the middle terms of the following binomial expansion (2x + 8y)5
Solution:
Given expansion is (2x + 8y)5
a = 2x,b = 8y, and n = 5
Middle terms will be (n – 1)/2 and (n + 1)/2
Tr + 1 = T (n – 1)/2 and T(n + 1)/2
First middle term:
Tr + 1 = T(n – 1)/2 = 5C(n – 1)/2.2x5 – (n – 1)/2.8y(n – 1)/2
T(5 – 1)/2 = 5C(5 – 1)/2.2x5 – (5 – 1)/2.8y(5 – 1)/2
T2 = 5C2.2x3.8y2
Second middle term:
Tr + 1 = T(n + 1)/2 = 5C(n + 1)/2.2x5 – (n + 1)/2.8y(n + 1)/2
T(5 + 1)/2 = 5C(5 + 1)/2.2x5 – (5 + 1)/2.8y(5 + 1)/2
T3 = 5C3.2x2.8y3
The middle terms of expansion are T2, and T3.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...