Gauss–Seidel method

This is to take Jacobi’s Method one step further. Where the better solution is x = (x1, x2, … , xn), if x1(k+1) is a better approximation to the value of x1 than x1(k) is, then it would better that we have found the new value x1(k+1) to use it (rather than the old value that isx1(k)) in finding x2(k+1), … , xn(k+1). So x1(k+1) is found as in Jacobi’s Method, but in finding x2(k+1), instead of using the old value of x1(k) and old values of x3(k),…, xn(k), we then use the new value x1(k+1) and the old values x3(k), … , xn(k), and similarly for finding x3(k+1), … , xn(k+1). This process to find the solution of the given linear equation is called the

Gauss-Seidel Method

The Gauss–Seidel method is an iterative technique for solving a square system of n (n=3) linear equations with unknown x. Given

Ax=B

, to find the system of equation x which satisfy this condition. In more detail, A, x and b in their components are :

Then the decomposition of A Matrix into its lower triangular component and its upper triangular component is given by:

The system of linear equations are rewritten as:

The Gauss–Seidel method now solves the left hand side of this expression for x, using previous value for x on the right hand side. More formally, this may be written as:

However, by triangular form of L*, the elements of x(k+1) can be computed sequentially using forward substitution:

This process is continuously repeated until we found the better approximated solution with least error.

Examples:

Input :
3
4x+ y+ 2z= 4
3x+ 5y+ 1z= 7
x+ y+ 3z= 3

Output :
[0, 0, 0]
[1.0, 0.8, 0.39999999999999997]
[0.6000000000000001, 0.9599999999999997, 0.48000000000000004]
[0.52, 0.9919999999999998, 0.49600000000000005]
[0.504, 0.9983999999999998, 0.4992000000000001]
[0.5008, 0.99968, 0.49984]
[0.5001599999999999, 0.9999360000000002, 0.4999679999999999]
[0.500032, 0.9999872, 0.4999936]
[0.5000064, 0.9999974400000001, 0.49999871999999995]
[0.50000128, 0.999999488, 0.4999997439999999]
[0.500000256, 0.9999998976000001, 0.49999994880000004]
[0.5000000512, 0.9999999795199999, 0.4999999897600001]
[0.50000001024, 0.999999995904, 0.499999997952]
[0.500000002048, 0.9999999991808, 0.49999999959040003]
[0.5000000004095999, 0.9999999998361601, 0.49999999991808003]
[0.50000000008192, 0.9999999999672321, 0.49999999998361594]
[0.500000000016384, 0.9999999999934465, 0.49999999999672307]
[0.5000000000032768, 0.9999999999986894, 0.4999999999993445]
[0.5000000000006554, 0.9999999999997378, 0.49999999999986894]
[0.500000000000131, 0.9999999999999478, 0.49999999999997374]
[0.5000000000000262, 0.9999999999999897, 0.49999999999999467]
[0.5000000000000052, 0.9999999999999979, 0.49999999999999895]
[0.5000000000000011, 0.9999999999999994, 0.49999999999999983]
[0.5000000000000002, 0.9999999999999998, 0.5000000000000001]
[0.49999999999999994, 1.0, 0.5]
[0.5, 1.0, 0.5]

Given the three equation:

4x + y + 2z = 4
3x + 5y + z = 7
x + y + 3z = 3

First we assume that the solution of given equation is

(0,0,0)

Then first we put value of y and z in equation 1 and get value of x and update the value of x as

(x1,0,0)

Now, putting the updated value of x that is x1 and z=0 in equation 2 to get y1 and then updating our solution as

(x1,y1,0)

Then, at last putting x1 and y1 in equation 3 to get z1 and updating our solution as

(x1,y1,z1)

Now repeat the same process 24 more times to get the approximate solution with minimum error.

Python3

# Defining our function as seidel which takes 3 arguments
# as A matrix, Solution and B matrix

def seidel(a, x ,b):
    #Finding length of a(3)
    n = len(a)
    # for loop for 3 times as to calculate x, y , z
    for j in range(0, n):
        # temp variable d to store b[j]
        d = b[j]

        # to calculate respective xi, yi, zi
        for i in range(0, n):
            if(j != i):
                d-=a[j][i] * x[i]
        # updating the value of our solution
        x[j] = d / a[j][j]
    # returning our updated solution
    return x

# int(input())input as number of variable to be solved
n = 3
a = []
b = []
# initial solution depending on n(here n=3)
x = [0, 0, 0]
a = [[4, 1, 2],[3, 5, 1],[1, 1, 3]]
b = [4,7,3]
print(x)

#loop run for m times depending on m the error value
for i in range(0, 25):
    x = seidel(a, x, b)
    #print each time the updated solution
    print(x)

An example for the matrix version A linear system shown as Ax=b is given by:

We want to use the equation

Where:

We must decompose A into the sum of a lower triangular component L* and a strict upper triangular component U:

The Inverse of L* is:

Now we can find remaining things:

Now we have T and C and we can use them to obtain the vectors x iteratively. First of all, we have to choose x{0} we can only guess. The better the guess, the quicker the algorithm will perform. We suppose:

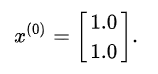
Then we can iteratively calculate other x{i’s}:

Now we know the Exact solution which matches the answer calculated above.

In fact, the matrix A is strictly diagonally dominant (but not positive definite).