Let A be the
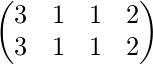
. What is the maximum value of x
TAx where the maximum is taken over all x that are the unit eigenvectors of A?
(A) 5
(B) (5 + √5)/2
(C) 3
(D) (5 – √5)/2
Answer: (B) Explanation: |M-λ.I| = 0, where λ is the eigen values and I is the identity matrix
|A-(λ*I)| = 0
(3-λ)(2-λ)-1 = 0
6-3λ -2λ + λ
2+1=0
λ
2-5λ+5=0
λ = (5+√5)/2 and (5-√5)/2,
λ = (5+√5)/2 is max value another root with negative sign which will not be max value.
For, λ=5+5√2, x
TAx=[18.131 21.231 21.231 34.331]
For, λ=5−5√2, x
TAx=
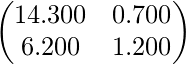
Hence, for λ=5+5√2 the value of x
TAx is maximum.
Quiz of this Question
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...