Interview Preparation
- Interview Preparation For Software Developers
- Must Coding Questions - Company-wise
- Must Do Coding Questions - Topic-wise
- Company-wise Practice Problems
- Company Preparation
- Competitive Programming
- Software Design-Patterns
- Company-wise Interview Experience
- Experienced - Interview Experiences
- Internship - Interview Experiences
Commerce
- Commerce
- Class 11 Accountancy Notes
- Class 12 Accountancy Notes
- Accountancy
- Class 11 Business Studies Notes
- Class 12 Business Studies Notes
- Business Studies
- Class 11 Microeconomics Notes
- Class 11 Statistics For Economics Notes
- Class 12 Macroeconomics Notes
- Class 12 Indian Economic Development Notes
- Economics
- Management
- Income Tax
- Finance
GATE | GATE IT 2006 | Question 86
Consider a database with three relation instances shown below. The primary keys for the Drivers and Cars relation are did and cid respectively and the records are stored in ascending order of these primary keys as given in the tables. No indexing is available in the database.
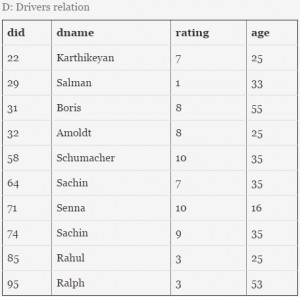
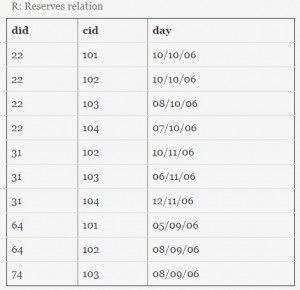
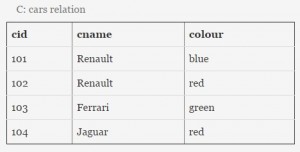 Let n be the number of comparisons performed when the above SQL query is optimally executed. If linear search is used to locate a tuple in a relation using primary key, then n lies in the range
Let n be the number of comparisons performed when the above SQL query is optimally executed. If linear search is used to locate a tuple in a relation using primary key, then n lies in the range


 Let n be the number of comparisons performed when the above SQL query is optimally executed. If linear search is used to locate a tuple in a relation using primary key, then n lies in the range
Let n be the number of comparisons performed when the above SQL query is optimally executed. If linear search is used to locate a tuple in a relation using primary key, then n lies in the range(A)
36 - 40
(B)
44 - 48
(C)
60 - 64
(D)
100 - 104
Answer
Please comment below if you find anything wrong in the above post
Feeling lost in the world of random DSA topics, wasting time without progress? It's time for a change! Join our DSA course, where we'll guide you on an exciting journey to master DSA efficiently and on schedule.
Ready to dive in? Explore our Free Demo Content and join our DSA course, trusted by over 100,000 geeks!
Last Updated :
Share your thoughts in the comments

GeeksforGeeks