GATE | GATE-CS-2003 | Question 6

Let T(n) be the number of different binary search trees on n distinct elements.
Then 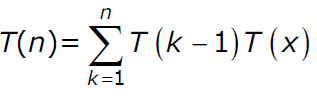, where x is
(A) n-k+1
(B) n-k
(C) n-k-1
(D) n-k-2


Answer: (B)

Explanation: The idea is to make a key root, put (k-1) keys in one subtree and remaining n-k keys in other subtree.

A Binary Search Tree (BST) is a tree in which all the nodes follow the below-mentioned properties −

• The left sub-tree of a node has a key less than or equal to its parent node’s key.
• The right sub-tree of a node has a key greater than to its parent node’s key.

Now construction binary search trees from n distinct number-
Lets for simplicity consider n distinct numbers as first n natural numbers (starting from 1)
If n=1 We have only one possibility, therefore only 1 BST.
If n=2 We have 2 possibilities , when smaller number is root and bigger number is the right child or second when the bigger number is root and smaller number as left child.

If n=3 We have 5 possibilities. Keeping each number first as root and then arranging the remaining 2 numbers as in case of n=2.

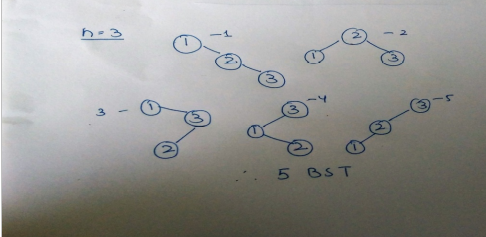
If n=4 We have 14 possibilities. Taking each number as root and arranging small numbers as left subtree and larger numbers as right subtree.

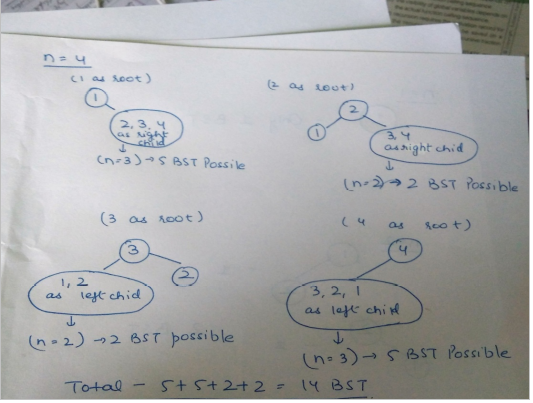
Thus we can conclude that with n distinct numbers, if we take ‘k’ as root then all the numbers smaller than k will left subtree and numbers larger than k will be right subtree where the the right subtree and left subtree will again be constructed recursively like the root.
Therefore,

This solution is contributed by Parul Sharma.

Quiz of this Question