GATE CS 2021 | Set 1

Question 1

Consider the following three functions.

f1 = 10n
f2 = nlogn
f3 = n√n 

Which one of the following options arranges the functions in the increasing order of asymptotic growth rate?

• f3,f2,f1
• f2,f1,f3
• f1,f2,f3
• f2,f3,f1

Question 2

Consider the following statements.

• S1: The sequence of procedure calls corresponds to a preorder traversal of the activation tree.
• S2: The sequence of procedure returns corresponds to a postorder traversal of the activation tree.

Which one of the following options is correct?

• S1 is true and S2 is false
• S1 is false and S2 is true
• S1 is true and S2 is true
• S1 is false and S2 is false

Question 3

Suppose that L1 is a regular language and L2 is a context-free language. Which one of the following languages is NOT necessarily context-free?

• L1∩L2
• L1⋅L2
• L1−L2
• L1∪L2

Question 4

The ratio of boys to girls in a class is 7 to 3. Among the options below, an acceptable value for the total number of students in the class is:

• 21
• 37
• 50
• 73

Question 5

A polygon is convex if, for every pair of points, P and Q belonging to the polygon, the line segment PQ lies completely inside or on the polygon. Which one of the following is NOT a convex polygon?

• A
• B
• C
• D

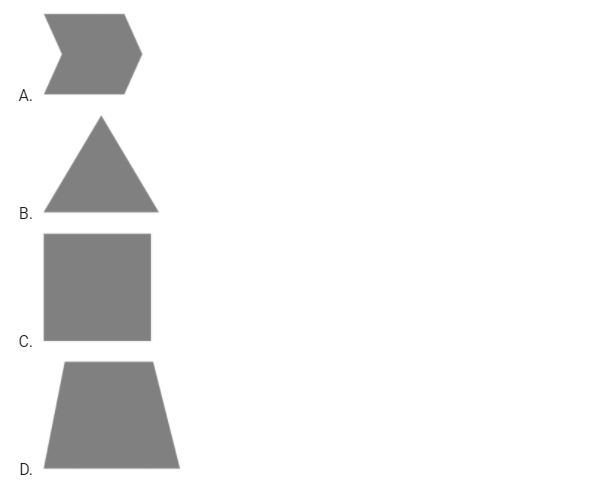
Question 6

Consider the following sentences:

• (i) Everybody in the class is prepared for the exam.
• (ii) Babu invited Danish to his home because he enjoys playing chess.

Which of the following is the CORRECT observation about the above two sentences?

• (i) is grammatically correct and (ii) is unambiguous
• (i) is grammatically incorrect and (ii) is unambiguous
• (i) is grammatically correct and (ii) is ambiguous
• (i) is grammatically incorrect and (ii) is ambiguous

Question 7

A circular sheet of paper is folded along the lines in the direction shown. The paper, after being punched in the final folded state as shown and unfolded in the reverse order of folding, will look like _______.

• A
• B
• C
• D

Question 8

___________ is to surgery as writer is to ___________ Which one of the following options maintains a similar logical relation in the above sentence?

• Plan, outline
• Hospital, library
• Doctor, book
• Medicine, grammar

Question 9

We have 2 rectangular sheets of paper, M and N, of dimensions 6 cm × 1 cm each. Sheet M is rolled to form an open cylinder by bringing the short edges of the sheet together. Sheet N is cut into equal square patches and assembled to form the largest possible closed cube. Assuming the ends of the cylinder are closed, the ratio of the volume of the cylinder to that of the cube is _________.

• π/2
• 3/π
• 9/π
• 3π

Question 10

Details of prices of two items P and Q are presented in the above table. The ratio of cost of item P to cost of item Q is 3:4. Discount is calculated as the difference between the marked price and the selling price. The profit percentage is calculated as the ratio of the difference between selling price and cost, to the cost

Profit% = ((Selling price – Cost)/Cost)×100 

The discount on item Q, as a percentage of its marked price, is _______ .

• 25
• 12.5
• 10
• 5