Game Theory (Normal-form Game) | Set 5 (Dominance Property-Mixed Strategy)

This article discusses how to solve a game by the dominance property with mixed strategy. Consider the below game:

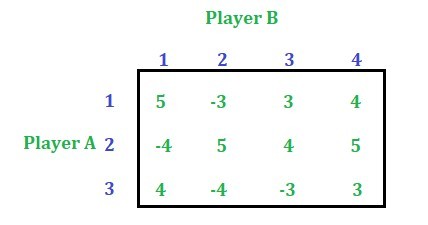
Solution: Find out the row minimum and column maximum values.

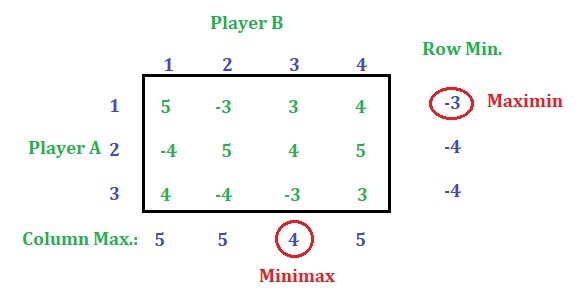
Here Minimax value is not equal to Maximin so this game has no saddle point. Now proceed with dominance property to reduce the rows and the columns.
Reducing the row and the column of the game is explained in this article. So, after reducing the rows and the columns, the following game will be left.

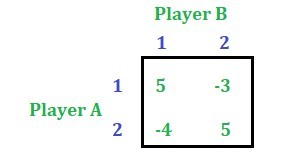
Note: We can also compare the elements of a particular row X with an average of two or more other rows and if the elements of row X are less than or equal to the corresponding elements after taking the average then delete the row X or we can also compare the elements of a particular column X with an average of two or more columns and if the elements of the column X are greater than the corresponding elements after taking the average then delete the column X.
Now solving this game using Mixed Strategy, we get,
– Value of the game = 0.76
– Probability of Player A = [9/17, 8/17, 0]
– Probability of Player B = [8/17, 9/17, 0]

My Personal Notes arrow_drop_up

Save